From the ALWS archives: A selection of papers from the International Wittgenstein Symposia in Kirchberg am Wechsel

1. Introduction

It is impossible for two different colors to occur at the same place simultaneously. Therefore if a simple color-statement that ascribes a color to a spatio-temporal location is true, then any simple color-statement that ascribes another color to the same spatiotemporal location cannot be true. But Wittgenstein's Tractatus logico-philosophicus (TLP) requires that elementary propositions must be logically independent of each other¹ (I'll call this "Independence Requirement"). Thus the Independence Requirement seems to conflict with the impossibility of simultaneous presence of different colors at the same place. This color-exclusion problem has been thought to be one of the main reasons why such a simple color-statement cannot be elementary proposition of TLP.

In this paper I shall show that such a simple color-statement can be analyzed into a truth-function of elementary propositions that are logically independent of each other. This means that we can construct a system of color-descriptions which satisfies the Independence Requirement, and it will turn out that our system of color-descriptions given below reflects "the logical structure of color" (TLP 6.3751) fairly well.

Some interpreters of TLP have tried to give an analysis of color-statements that can solve the color-exclusion problem. But they don't seem to be successful. Canfield's analysis (1976, 90-93), which attempts to make the logic of color-mixture overlap with that of truth-functions (Cook also follows this line (1994, 37-39)), I think, cannot handle the color-metamerism² adequately. For it turns out that the Independence Requirement must be given up in so far as the metamerism is taken into account. Wedin's analysis (1992, 51-52), which follows faithfully a passage from Wittgenstein's Big Typescript (TS213, 475-476), cannot overcome the same problem as Canfield's analysis encounters. Hintikka & Hintikka offer, "as a thought-experiment", a color-ascription by "a function c which maps points in visual space into a color space" (1986, 121-124). But this proposal will encounter two difficulties : (a) it cannot satisfy the Independence Requirement ; (b) it would give rise to a contradiction that is not truth-functional but is "logical", to the contrary of TLP (6.375,5.525,4.46).

Now the multiplicity of colors can be depicted by various figures such as a line (according to the color-spectrum), a circle (e.g., Newton's color-circle), a plane figure whose shape looks like a sail of a sailboat (the chromaticity-diagram of the CIE), an octahedron (according to hue and lightness), and various solid bodies (according to hue, lightness, and saturation), &c. The analysis of color-statements in the next section, which relies on a notation which I call the "dividing notation", should be, and indeed is independent of which figure we use to depict the color-multiplicity. In order to make this clear, I shall present the notation in a general form (§2), and then apply it to a particular color-space (§3).

2. Dividing notation in its general form

As is seen below, the dividing notation relies on the binary-notation. The idea of using the binary-notation to describe colors has been suggested by Wittgenstein (Z, §368). Carruthers used this idea to construct a model of color-descriptions that satisfies the Independence Requirement (1990, 144-147)³. He exhibited the model whose color-space is only 1-dimensional (yet he doesn't adopt it eventually, since his interpretation of TLP isn't "phenomenalist"). I will generalize this idea into the "dividing notation" and will show that this notation is applicable to any (finite) n-dimensional space.

Suppose the color-multiplicity is depicted by a (finite) n-dimensional space Q = Q₁×Q₂×.... ×Q_n adequately, a value of each Q_m(1 ≤ m ≤ n) corresponds to an intensity of a piece of various features of color (e.g., hue, lightness, &c.), and it ranges over within the closed interval [0,1]. Thus the color-space Q can be defined as

• { <x₁,...,x_n> | x₁∈Q₁ & .... & x_n∈Q_n & 0 ≤ x₁ ≤ 1 & .... & 0 - x_n - 1 },

where every color corresponds to an ordered n-tuple <x₁,...,x_n> ∈Q.

Now, for a natural number m (1 ≤ m ≤ n), consider the following function D_m from Q into { 0, 1 } :

This function assigns 0 to <x₁,...,x_n> ∈Q if 0 ≤ x_m ≤ 0.5 and assigns 1 to it otherwise. This operation that assigns 0 or 1 to every n-tuple <x₁,...,x_n> ∈Q according to the value of its m-th member x_m just corresponds to the operation that divides the n-dimensional color-space in two with respect to the m-th dimension and assigns 0 to one section generated by the division and 1 to the other. So this function can be called a "dividing function". Thus the n-dimensional color-space Q is divided by each of these n dividing functions.

Next, for a natural number m (1 ≤ m ≤ n), consider the following function D_n+m from Q into { 0, 1 } :

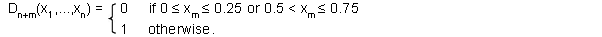
This function assigns 0 to <x₁,...,x_n> ∈Q if 0 ≤ x_m ≤ 0.25 or 0.5 < x_m ≤ 0.75 and assigns 1 to it otherwise. So this function divides the color-space Q finer than the previous n dividing functions. If we repeat this kind of division n+n times, then we assign to every n-tuple <x₁,...,x_n> ∈Q a following binary-decimal up to the n+n-th place :

• .D₁....D_nD_n+1....D_n+n ( .D₁(x₁,...,x_n)....D_n(x₁,...,x_n)D_n+1(x₁,...,x_n)....D_n+n(x₁,...,x_n) ).

We can divide the color-space Q as many times as we like. And the more times it is divided, the finer the differences of colors are articulated. If it is divided k times, then a binary-decimal up to the k-th place is assigned to each section generated by the k times of division and different decimals are assigned to different sections. Therefore if we specify a binary-decimal (up to the k-th place), we can specify a particular color that corresponds to the section to which it is assigned.

Then elementary propositions take the form

• PTm

which says that

• (#) A color <x₁,...,x_n> occurs at the place P at the time T , where that color corresponds to one of the sections to which a binary-decimal having '1' at the m-th place is assigned.

And in order to specify a color that corresponds to a section to which a binary-decimal having '0' at the m-th place is assigned, we will use the negation "¬PTm" of "PTm". So if a color <x₁,...,x_n> is located in a section of Q to which the binary-decimal .01001.... is assigned, i.e., it is the case that

• ₁(x₁,...,x_n)=0, D₂(x₁,...,x_n)=1, D₃(x₁,...,x_n)=0, D₄(x₁,...,x_n)=0, D₅(x₁,...,x_n)=1, ....,

then the statement "a color <x₁,...,x_n> occurs at the place P at the time T" is analyzed into the proposition "¬PT1 & PT2 & ¬PT3 & ¬PT4 & PT5 & ....".

The dividing notation here has been formulated in its general form. In the next section, I will apply it to a particular color-space and construct a concrete system of color-descriptions.

3. The color-exclusion problem revisited

First, assume that four colors Red, Yellow, Blue, and Green are elementary (cf., WWK, 42), and consider a color-square with its four vertexes corresponding to those four elementary colors respectively. Then regard this color-square as a coordinate-space whose origin is the vertex to which, for example, Yellow corresponds (Fig.1).

Fig.1

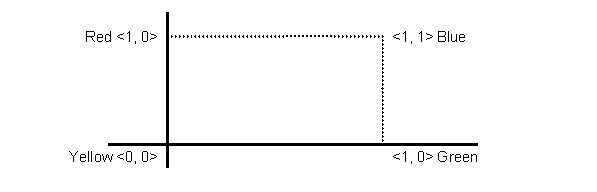
Thus we've got a 2-dimensional color-space Q whose x-axis is Yellow-Green and whose y-axis is Yellow-Red (we call the former "Q_x", the latter "Q_y". Therefore Q = Q_x×Q_y). Here we have the color space :

• { <x, y> | x∈Q_x & y∈Q_y & 0 ≤ x ≤ 1 & 0 ≤ y ≤ 1 },

and now every color corresponds to an ordered pair <x, y> ∈Q (the distance from the point <x, y> to, for instance, a vertex <0, 1> depicts Red content of the color <x, y> ).

Now I will divide this color-space Q into sixteen sections by the following four dividing functions (from Q into { 0, 1 }) :

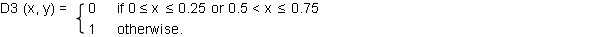
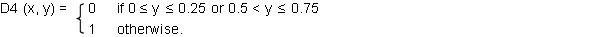
Each of these functions assigns 0 or 1 to every <x, y> ∈Q according to the value of x or y. By these functions a binary-decimal up to the 4-th place

• .D₁D₂D₃D₄ ( .D₁(x, y)D₂(x, y)D₃(x, y)D₄(x, y) )

is assigned to every <x, y> ∈Q. In other words, every color <x, y> is located in a section .D₁D₂D₃D₄ of the 2-dimensional color-space Q. Introducing these four dividing functions amounts to fitting our color-space Q with the grid shown in the following figure.

Fig. 2

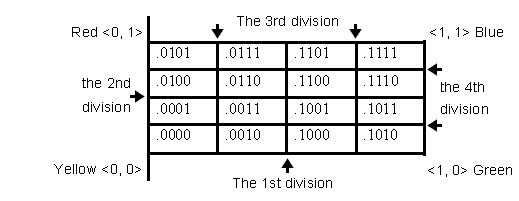
What an elementary proposition "PTm" says is just like (#) in §2 except n = 2, and a negated elementary proposition is used in the same way as in §2. Then since the color Red corresponds to the ordered pair <0, 1> in the above figure, and it is the case that

• D₁(0, 1) = 0, D₂(0, 1) = 1, D₃(0, 1) = 0, and D₄(0, 1) = 1

( i.e., Red is located in the section .0101 of Q), the statement "Red occurs at the place P at the time T " is analyzed into the proposition "¬PT1 & PT2 &¬PT3 & PT4". As is easily shown, elementary propositions are now independent of each other. Every (negated) elementary proposition doesn't imply any (negated) elementary proposition except itself (e.g., even if "PT1" is true, that doesn't imply either "PT2 " or "¬PT2 " is true).

And it is noteworthy that any statement that ascribes different colors to the same spatio-temporal location can now be shown to be a genuine truth-functional contradiction (cf., TLP6.3751). For example, the statement "Red and Blue occur at the place P at the time T " is analyzed into the genuine truth-functional contradiction : (¬PT1 & PT2 &¬PT3 & PT4 ) & (PT1 & PT2 & PT3 &PT4 ).

Moreover, from a proposition that ascribes a certain color to a certain spatio-temporal location we can deduce a negation of a proposition that ascribes another color to the same spatio-temporal location. In other words, the latter is a logical consequence of the former (under the classical two-valued propositional logic, of course). For example, the statement "Red occurs at the place P at the time T" can be analyzed into the proposition "¬PT1 & PT2 &¬PT3 &PT4 ". This clearly implies "¬(¬PT1 &¬PT2 &¬PT3 &¬PT4 )", which is the negation of the proposition corresponds to the statement "Yellow occurs at the place P at the time T ". —Thus we can see that our system of color-descriptions reflects "the logical structure of color" (TLP6.3751) fairly well.

4. Conclusion

The dividing notation, as we have seen, enables us to construct a system of color-descriptions that satisfies the Independence Requirement and reflects "the logical structure of color" (TLP 6.3751) fairly well. The dividing notation will be applicable not only to a system of color-descriptions but also to the systems of statements that describe sensory qualities of any kind (if its multiplicity can be mapped into a (finite) n-dimensional space⁴). Therefore we can conclude that the "completely analyzed" language of TLP (3.201,3.25) can have empirical content even with the Independence Requirement.