Transcriber(s): Michael Biggs, Peter Cripps
Proofreader(s): Peter Cripps
Comments:
Transcriptions of material from The Bertrand
Russell Archives, McMaster University, Canada;
their catalogue no.s:
TS section (pp. numbered 1-7) - RA1.710.057822,
MS section (pp. numbered 1-23 plus 3 unnumbered
folios) - RA1.710.057823.
This item consists of two parts: a typescript of
7ff. with corrections in Russell´s hand and
additions in Wittgenstein´s hand, and a manuscript
of 26ff. in Russell´s hand. In the TS part:
non-typewriter characters are inserted by hand;
fully typed pages have 24 or 25 lines of type;
each new sentence is separated from the last by
three spaces. True double spaced blank lines used
occasionally but not consistently.
Hands:
s = handwritten insertions that belong to first
pass, ie generally the insertion of symbols which
are not found on the typewriter such as φ and &Exist;,
H5 = Ludwig Wittgenstein, or cases where the
transcriber has felt unable to decide whether
Ludwig Wittgenstein or Bertrand Russell
S1 = Bertrand Russell
� Item 201a-1 Recto Page A1
1

‹Summary›1
The2 One1 reason for thinking the old
notation wrong is that it is very unlikely that
from every proposition p an infinite number of
other propositions not-not-p, not-not-not-not-p,
etc., should follow.
If only th[e|o3]se signs which contain proper
names were complex then propositions containing
nothing but apparent variables would be simple.
Then what about their denials?
The verb of a proposition cannot be "is true"
or "is false", but whatever is true or false must
already contain the verb.
The2 [d|D3]eductions only proceed according
to the laws of deduction‹,›4 but these laws cannot
justify the deduction.
The2 One1 reason for supposing that not all
propositions which have more than one argument are
relational propositions is that «if»1 they
were‹,›1 the relations of judgement and inference
that2 would1 have to hold between an arbitrary
number of things.
Every proposition which seems to be about a
complex can be analysed into a proposition about
those2 «its»1 cons[i|t]ituents and about the
proposition which describes a2 the1 complex
perfectly; i.e., that proposition which is
equivalent to saying a2 the1 complex exists.
The idea that propositions are names of
complexes between5 L.W.4 suggestions5‹s›4 <?>6
L.W.4 that whatever is not a proper name is a sign
for a relation. ‹Because spatial complexes*
consist of Things & Relations only & the idea of a
complex is taken from sp›4
In a proposition convert all its indefinables
into variables; there then remains a class of
propositions which has2 is1 not all propositions
but a type.
<* you7 - for instance imagine every fact as a
spatial complex>8
Item 201a-1 Recto Page A2
2
There are thus two ways in which signs are
similar. The names Socrates and Plato are similar:
they are both names. But whatever they have in
common must not be introduced before Socrates and
Plato are introduced. The same applies to
subject-predicate form etc. Therefore, thing,
proposition, subject-predicate form, etc., are not
indefinables, i.e., types are not indefinables.

When we say a2 A1 judge‹s›1 is2 that etc.,
then we have to mention a whole proposition which
a2 A1 judge‹s›1 is2. It will not do either to
mention only its constituent‹s,›1 or its
constituent‹s›1 and form, but not in the proper
order. This shows that a proposition itself must
occur in the statement that it is judged; however,
for instance, "not-p" may be explained[.|,9] ‹p10
must occur in it.›1 5 <[t|T9]he question, "What is
negated" must have a meaning>11
Always a que[x|s]tion that is negated must
have a meaning.5 <Rott!>12
To understand a proposition p it is not
enough to know that "5p implies ‹´"›4p" is
true‹´›4, but we must also know that p also
implies ‹´›4"not-p" is false‹´›4 5 ˜p implies "p
is false"4. This shows the «bi»13polarity of the
proposition.
<W-F = Wahr-Falsch>6
To every molecular function «a»1 [wf|WF3]
scheme corresponds. Therefore we may use the
[wf|WF3] scheme itself instead of the function.
Now what the [wf|WF3] scheme does is, it
correlates the letters [w|W3] and [f|F3] with each
proposition. These two letters are the poles of
atomic propositions. Then «the scheme»1
corresponds2lates1 another [f|W3] and [w|F3] to
these poles. In this notation all that it2 matters
is the correlation of the outside poles to the
pole of its2 «the»1 atomic propositions. Therefore
not-not-p is the same symbol as p. ‹And›1
Therefore we shall never get two symbols for the
same molecular functions5.
Item 201a-1 Recto Page A3
3
The meaning of a proposition is the fact
which actually corresponds to it.
As the ab functions of atomic propositions
are by2i1‹-›1polar propositions again we can
perform ab7 operations on them. We [wi|sha9]ll‹,›4
b[e|y9] doing so, correlate two new outside poles
via the old outside poles to the poles of the
atomic propositions.
The symbolising fact in a-p-b is that, say7*
a7 is on the left of p7 and b7 on the right of
p7[,|;9] then the correlation of new poles is to
be transitive, such2 so1 that «for instance»4 if a
new pole a7 in whatever way «i.e. via whatever
poles»4 is correlated to the inside a7, the symbol
is not changed thereby. It is therefore possible
to construct all possible ab7 functions by
performing one ab7 operation repeatedly, and we
can therefore talk of all ab7 functions as of all
th[e|o9]se functions which can be obtained by
performing this ab7 operation repeatedly.
<[Note by B.R.]>6
[NB. ab7 means the same as [wf|WF3], which
means true-false.]

Naming is like pointing. A function is like a
line dividing points «of a plane»4 into right and
left ones; then ‹"›1p or not-p‹"›1 has no meaning
because it does not divide [a|the9] plane.
But though a particular proposition "p"5 or a
"5not-p" has no meaning‹,›4 a general proposition
‹"›4for all p´s, "5p"5 or "5not-p" has a meaning
because this does not contain [a|the9] nonsensical
function ‹"›4p [n|o]r not-p‹"›4 but [a|the9]
function ‹"›4p or "5not-q" just as ‹"›4for all
"5x´s xRx‹"›1 contains the function ‹"›4xRy".
<* This is quite arbitrary but if we such have
fixed on which sides the poles have to stand we
must of course stick to our convention. If for
instance "apb" says p then bpa says nothing7. (It
does not say ˜p) But a-apb-b is the same symbol as
apb>8
<the ab function vanishes automatically) for here
the new poles are>14 <related to the same side of
p as the old ones. The question is allways: how
are the new poles correlated to p compared with
the way the old poles are correlated to p.>15
Item 201a-1 Recto Page A4
4
A proposition is a standard to which all
facts behave, that2 with1 names it «is»1
otherwise; it is then2us1 by2i1‹-›1polarity and
sense comes in‹;›1 just as one error2 arrow1
behaves to another error2 arrow1 by being in the
same sense or the opposite, so a fact behaves to a
proposition.

The form of a proposition has meaning in the
following way. Consider a symbol ‹"›4xRy‹"›4. To
symbols of this form correspond couples of things
whose names are respectively ‹"›4x‹"›4 and
‹"›4y‹"›4. The things x7‹/›4y7 stand to one
another in all sorts of relations‹,›4 amongst
others some stand in the relatio[j|n] of2 R1, and
some not; just as I single out a particular thing
by a particular name I single out all behaviours
of the point‹s›1 x and y the one between2 with
respect to1 the relation ‹R.›1 of the other2. I
say that if an x stands in the relation of2 R1 to
a y the sign ‹"›4x of2 R1 y‹"›4 is to be called
true to the fact and otherwise false. This is a
definition of sense.
<!>16
In my theory p has the same meaning as not-p
but opposite snese. The meaning is the fact. The
proper theory of judgment must make it impossible
to judge nonsense.
It is not strictly true to say that we
understand a proposition p if we know that p is
equivalent to "p is true" for this would be the
case if accidentally both were true or false. What
is wanted is the formal equivalence with respect
to the forms of the proposition[.|,9] i.e.,
[A|a9]ll the general indefinables involved. The
sense of an ab7 function of a proposition is a
function of its sense[:|.9] [t|T9]here are only
unasserted propositio‹ns.›4
Item 201a-1 Recto Page A5
5
Assertion is merely psychological. If2n1 not-p‹,›1
«p10»1 is exactly the same as if it stands
alone‹;›1 this point is absolutely fundamental.
Among the facts which make "p or q" true1 there
are also facts which make "p and q" true‹;›1 if
propositions do only mean2 «have only
meaning»1‹,›1 we ought‹,›1 to know2 «in»1 such a
case, to1 say that these two propositions are
identical, but in fact, their sense is different
for we have introduced sense by talking of all p´s
and all q´s. Consequently the molecular
propositions will only be used in cases where
there ab7 function stands under a generality sign
or enters into another function such as ‹"›4I
believe that, etc.,‹"›4 because then4 the sense
enters.
In "a judges p" p cannot be replaced by a
proper name. This appears if we substitute "a
judges that p is true and not p is false". The
proposition "a judges p" consists of the proper
name a[.|,9] [T|t9]he proposition p with its 2
poles‹,›4 and a7 being related to both of these
poles in a certain way. This is obviously not the5
‹a›4 relation in the ordinary sense.
The ab notation and5 for4 apparent variables5
make‹s›4 it clear that not and or are dependent on
one another and we can therefore not use them as
simultaneous indefinables. ‹|17›4 Some5 ‹Same›4
objections «in the case of app. var.»4 to old
indefinables, [a|A9]s5 as4 18 in the case of
molecular functions19[,|:9] [t|T9]he application
of the ab notation to apparently5‹-›4 variable
propositions become‹s›4 clear if we consider that,
for instance, the proposition ‹"›4for all "5x‹,›4
φx" is to be true when φx is true for all x´s and
false when φx is false for some x´s. We see that
some and all occur simultaneously in the proper
apparent variable notation.
Item 201a-1 Recto Page A6
6
The Notation is:
for (x) φx ; a - (x) - a φ x b - (&Exist; x) - b
and
for (φ5&Exist;x) φ x : a - (&Exist;x) - a φ x b - (x) - [v|b]

Old definitions now become tautologous.
In aRb it is not the complex that symbolises
but the fact that the symbol a stands in a certain
relation to the symbol b. Thus facts are
symbolised by facts, or the5 more correctly: that
a certain thing is the case in the symbol says
that a certain thing is the case in the world.
Judgment, question and command are all on the
same level. What interests logic in them is only
the unasserted proposition. Facts cannot be named.

A proposition cannot occur in itself. This is
the fundamental truth of the theory of types.

Every proposition that says something
important5 about one thing is a subject-predicate
proposition, and so on.
Therefore we can recognize a
subject-predicate proposition if we know it
contains only one name and one form, etc. This
gives the construction of types. Hence the type of
a proposition can be recognized by its symbol
alone.
Item 201a-1 Recto Page A7
7
What is essential in a correct
apparent«-variable»1 notation is this:- (1) it
must mention a type of propositions; (2) it must
show which components of a proposition of this
type are constants.@

[Components are forms and constituents.]

Take (φ).φ!x. Then if we describe the kind7
of symbols20«, for which φ! stands»4 ‹&›4 which,
by the above, is enough to determine the type,
then automatically "([x|φ]).φ!x" cannot be
fi[ll|tt]ed by this descri[l|p]tion[.|,9] ‹because
it contains7 "φ!x" & the description is to
describe all7 that symbolizes in symbols of the φ!
- kind. If the description is thus7 complete
vicious circles can just as little occur as if5
for instance in (φ).φ(x)5 (φ).(x)φ4 (where (x)φ is
a subject-predicat prop) ›4
Item 201a-1 Recto Page B1
Wittgenstein 1

First MS.
Indefinables are of two sorts: names, & forms.
Propositions cannot consist of names alone; they
cannot be classes of names. A name can not only
occur in two different propositions, but can
occur in the same way in both.
Propositions [which are symbols having
reference to facts] are themselves facts: that
this inkpot is on this table may express that I
sit in this chair.
It can never express the common
characteristic @ of two objects that we denote
designate them by the same name but by two
different ways of designation, for, since names
are arbitrary, we might ‹also› choose different
names, & where then would be the common element
in the designations? Nevertheless one is always
tempted, in a difficulty, to take refuge in
different ways of designation. @
Frege said "propositions are names";
Russell said "propositions correspond to
complexes". Both are false; & especially false
is the statement "propositions are names of
complexes".
It is easy to suppose that only such
symbols are complex as contain names of objects
objects, & «that accordingly» "(&Exist;x,φ).φx" or
"(&Exist;x,«R,»y).xRy" must be simple. It is then
natural to call the first of these the name of a
form, the second the name of a relation. But in
that case what is the meaning of (e.g.)
"˜(&Exist;x,y).xRy"? Can we put "not" before a name?
Item 201a-1 Recto Page B2
Wittg.- 2
The reason why "˜Socrates" means nothing is
that "˜x" does not express a property of x.
There are positive & negative facts: if the
proposition "this rose is not red" is true, then
its «what it» signifies is negative. But the
occurrence of the word "not" does not indicate
this unless we know that the signification of
«the proposition» "this rose is red" (when it is
true) is positive. It is only from both, the
negation & the negated proposition, that we can
conclude to a characteristic of the significance
of the whole proposition. (We are not here
speaking of negations of general propositions,
i.e. of such as contain apparent variables.)
Negative facts only justify the negations of
simpl atomic propositions.)
Positive & negative facts there are, but
not true & false facts.
If we overlook the fact that propositions
have a sense which is independent of their truth
or falsehood, it easily seems as if true & false
were two equally justified relations between the
sign & what is signified. (We might then say
e.g. that "q" signifies in the true way what
"not-q" signifies in the false way). But are not
true & false in fact equally justified? Could we
not express ourselves by means of false
propositions just as well as hitherto with true
ones, so long as we know that they are meant
falsely?
Item 201a-1 Recto Page B3
3
No! For a proposition is then true when it is as
we assert in this proposition; & accordingly if
by "q" we mean "not-q", & it is as we mean to
assert, then in the new interpretation "q" is
actually true & not false. But it is important
that we can mean the same by "q" as by "not-q",
for it shows that neither to the symbol "not"
nor to the manner of its combination with "q"
does a characteristic of the denotation of "q"
correspond.
Item 201a-1 Recto Page B4
4

2nd MS.
We must be able to understand propositions which
we have never heard before. But every
proposition is a new symbol. Hence we must have
general indefinable symbols; these are
unavoidable if propositions are not all
indefinable.
Whatever corresponds in reality to compound
propositions must not be more than what
corresponds to their several atomic
propositions.
Not only must logic not deal with
[particular] things, but just as little with
relations & predicates.
There are no propositions containing real
variables.
What corresponds in reality to a
proposition depends upon whether it is true or
false. But we must be able to understand a
proposition without knowing if it is true or
false.
What we know when we understand a
proposition is this: We know what is the case if
the proposition is true, & what is the case if
it is false. But we do not know [necessarily]
whether it is true or false.
Propositions are not names.
We can never distinguish one logical type
from another by attributing a property to
members of the one which we deny to members of
the other.
Symbols are not what they seem to be. In
"aRb", "R" looks like a substantive, but is not
one. What symbolizes in "aRb" is that R occurs
between a & b. Hence "R" is not the indefinable
in "aRb". Similarly in "φx", "φ" looks like a
substantive but is not one; in "˜p", "˜" looks
like "φ" but is not like it. This is the first
thing that indicates that there may not be
logical constants. A reason against them is the
generality of logic: logic cannot treat a
special set of things.
Item 201a-1 Recto Page B5
Wittg.- 5
Molecular propositions contain nothing
beyond what is contained in their atoms; they
add no material information above that contained
in their atoms.
All that is essential about molecular
functions is their T-F schema [i.e. the
statement of the cases when they are true & the
cases when they are false].
Alternative indefinability shows that the
indefinables have not been reached.
Every proposition is essentially
true-false: to understand it, we must know both
what must be the case if it is true, & what must
be the case if it is false. Thus a proposition
has two poles, corresponding to the case of its
truth & the case of its falsehood. We call this
the sense of a proposition.
In regard to notation, it is important to
note that not every feature of a symbol
symbolizes. In two molecular functions which
have the same T-F schema, what symbolizes must
be the same. In "not-not-p", "not-p" does not
occur; for "not-not-p" is the same as "p", &
therefore, if "not-p" occurred in "not-not-p",
it would occur in "p".
Logical indefinables cannot be predicates
or relations, because propositions, owing to
sense, cannot have predicates or relations. Nor
are "not" & "or", like judgment, analogous to
predicates or relations, because they do not
introduce anything new.
Propositions are always complex even if
they contain no names.
Item 201a-1 Recto Page B6
6
A proposition must be understood when all
its indefinables are understood. The
indefinables in "aRb" are introduced as follows:
"a" is indefinable;
"b" is indefinable;
Whatever "x" & "y" may mean, "xRy" says
something indefinable21 about their meanings.
A complex symbol must never be introduced
as a single indefinable. (Thus e.g. no
proposition is indefinable.) For if one of its
parts occurs also in another connection, it must
there be re-introduced. And would it then mean
the same?
The ways by which we introduce our
indefinables must permit us to construct all
propositions that have sense [? meaning] from
these indefinables alone. It is easy to
introduce "all" & "some" in a way that will make
the construction of (say) "(x,y).xRy" possible
from "all" & "xRy" as introduced before.
Item 201a-1 Recto Page B7
Wittg.- 7

3rd MS.
A comparis An analogy for the theory of truth:
Consider a black patch on white paper; then we
can describe the form of the patch by
mentioning, for each point of the surface,
whether it is white or black. To the fact that a
point is black corresponds a positive fact, to
the fact that a point is white (not black)
corresponds a negative fact. If I designate a
point of the surface (one of Frege´s
"truth-values"), this is as if I set up an
assumption to be decided upon. But in order to
be able to say of a point that it is black or
that it is white, I must first know when a point
is to be called black & when it is to be called
white. In order to be able to say that "p" is
true (or false), I must first have determined
under what circumstances I call a proposition
true, & thereby I determine the sense of a
proposition. The point [on|in] which the analogy
depends fails is this: I can indicate a point of
the paper what is white & black, but to a
proposition without sense nothing corresponds,
for it does not designate a thing (truth-value),
whose properties might be called "false" or
"true"; the verb of a proposition is not "is
true" or "is false", as Frege believes, but what
is true must already contain the verb.
The comparison of language & reality is
like that of retinal image & visual image: to
the blind spot nothing in the visual image seems
to correspond, & thereby the boundaries of the
blind spot determine the visual image - as true
negations of atomic propositions determine
reality.
Item 201a-1 Recto Page B8
Wittg.- 8
Logical inferences can, it is true, be made
in accordance with Frege´s or Russell´s laws of
deduction, but this cannot justify the
inference; & therefore they are not primitive
propositions of logic. If p follows from q, it
can also be inferred from q, & the "manner of
deduction" is indifferent.
Those symbols which are called propositions
in which "variables occur" are in reality not
propositions at all, but only schemes of
propositions, which only become propositions
when we replace the variables by constants.
There is no proposition which is expressed by "x
= x", for "x" has no signification; but there is
a proposition "(x).x = x" & propositions such as
"Socrates = Socrates" etc.
In books on logic, no variables ought to
occur, but only the general propositions which
justify the use of variables. It follows that
the so-called definitions of logic are not
definitions, but only schemes of definitions, &
instead of these we ought to put general
propositions; & similarly the so-called
primitive ideas «(Urzeichen)» of logic are not
primitive ideas, but the schemes of them. The
mistaken idea that there are things called facts
or complexes & relations easily leads to the
opinion that there must be a relation of
questioning to the facts, & then the question
arises whether a relation can hold between an
arbitrary number of things, since a fact can
follow from arbitrary cases. It is a fact that
the proposition which e.g. expresses that q
follows from p & p⊂q is this: p.p⊂q.⊂p.q.q.
Item 201a-1 Recto Page B9
Wittg.- 9
At a pinch, one is tempted to interpret
"not-p" as "everything else, only not p". That
from a single fact p an infinity of others,
not-not-p etc., follow, is hardly credible. Man
possesses an innate capacity for constructing
symbols with which some sense can be expressed,
without having the slightest idea what each word
signifies. The best example of this is
mathematics, for man has until lately used the
symbols for numbers without knowing what they
signify or that they signify nothing.
Russell´s "complexes" were to have the
useful property of being compounded, & were to
combine with this the agreeable property that
they could be treated as «like» "simples". But
this alone made them unserviceable as logical
types, since there would have been significance
in asserting, of a simple, that it was complex.
But a property cannot be a logical type.
Every statement about apparent complexes
can be resolved into the logical sum of a
statement about the constituents & a statement
about the proposition which describes the
complex completely. How, in each case, the
resolution is to be made, is an important
question, but its answer is not unconditionally
necessary for the construction of logic.
Item 201a-1 Recto Page B10
Wittg.- 10
That "or" & "not" etc. are not relations in
the same sense as "right" & "left" etc., is
obvious to the plain man. The possibility of
cross-definitions in the old logical
indefinables shows, of itself, that these are
not the right indefinables, &, even more
conclusively, that they do not denote relations.
If we change a constituent a of a
proposition φ(a) into a variable, then there is
a class
˜p {(&Exist;x).φ(x) = p}.
This class in general still depends upon what,
by an arbitrary convention, we have mean by
"φ(x)". But if we change into variables all
those symbols whose significance was arbitrarily
determined, there is still such a class. But
this is now not dependent upon any convention,
but only upon the nature of the symbol "φ(x)".
It corresponds to a logical type.
Types can never be distinguished from each
other by saying (as is often done) that one has
th[i|e]s‹e› @ but the other has th[at|ose]
propert[y|i]‹es›, for this presupposes that
there is a meaning in asserting all these
properties of both types. But from this it
follows that, at best, these properties may be
types, but certainly not the objects of which
they are asserted.
Item 201a-1 Recto Page B11
Wittg.- 11
At a pinch, we are always inclined to
explanations of «logical» functions of
propositions which «aim at introducing into the
function» either only contain the constituents
of these propositions, or only their forms, etc.
etc; & we overlook that ordinary language would
not contain the whole propositions if it did not
need them: However, e.g., "not-p" may be
explained, there must always be a meaning given
to the question "what is denied?"
The very possibility of Frege´s
explanations of "not-p" & "if p then q", from
which it follows that "not-not-p" denotes the
same as p, makes it probable that there is some
method of designation in which "not-not-p"
corresponds to the same symbol as "p". But if
this method of designation suffices for logic,
it must be the right one.
Names are points, sentences propositions
arrows - they have sense. The sense of a
proposition is determined by the two poles true
& false. The form of a proposition is like a
straight line, which divides all points of a
plane into right & left. The line does this
automatically, the form of proposition only by
convention.
Item 201a-1 Recto Page B12
Wittg.- 12
Just as little as we are concerned, in
logic, with the relation of a name to its
meaning, just so little are we concerned with
the relation of a proposition to reality, but we
want to know the meaning of names & the sense of
propositions - as we introduce an indefinable
concept "A" by saying: "´A´ denotes something
indefinable", so we introduce e.g. the form of
propositions aRb by saying: "For all meanings of
"x" & "y", "xRy" expresses something indefinable
about x & y".
In place of every proposition "p", let us
write @ "abp". Let every correlation of
propositions to each other or of names to
propositions be effected by a correlation of
their poles "a" & "b". Let this correlation be
transitive. Then accordingly "a-ab-bp" is the
same symbol as "abp". Let n propositions be
given. I then call a "class of poles" of these
propositions every class of n members, of which
each is a pole of one of the n propositions, so
that one member corresponds to each proposition.
I then correlate with each class of poles one of
two poles (a & b). The sense of the symbolizing
fact thus constructed I cannot define, but I
know it.
If p = not-not-p etc., this shows that the
traditional method of symbolism is wrong, since
it allows a plurality of symbols with the same
sense; & thence it follows that, in analyzing
such propositions, we must not be guided by
Russell´s method of symbolizing.
Item 201a-1 Recto Page B13
Wittg.- 13
It is to be remembered that names are not
things, but classes: "A" is the same letter as
"A". This has the most important consequences
for every symbolic language.
Neither the sense nor the meaning of a
proposition is a thing. These words are
incomplete symbols.
It is impossible to dispense with
propositions in which the same argument occurs
in different positions. It is obviously useless
to replace φ(a,a) by φ(a,b).a = b.
Since the ab-functions of p are again
bi-polar propositions, we can form ab-functions
of them, & so on. In this way a series of
propositions will arise, in which in general the
symbolizing facts will be the same in several
members. If now we find an ab-function of such a
kind that by repeated application of it every
ab-function can be generated, then we can define
introduce the totality of ab-functions as the
totality of those that are generated by
application of this function. Such a function is
˜pv˜q.
Item 201a-1 Recto Page B14
Wittg.- 14

It is easy to suppose a contradiction in
the fact that on the one hand all every possible
complex proposition is a simple ab-function of
simple propositions, & that on the other hand
the repeated application of one ab-function
suffices to generate all these propositions. If
e.g. an affirmation can be generated by double
negation, is negation in any sense contained in
affirmation? Does "p" deny "not-p" or assert
"p", or both? And how do matters stand with the
definition of "⊂" by "v" & "˜" ".", or of "v" by
"." & "⊂"? And how e.g. shall we introduce p|q
(i.e. ˜pv˜q), if not by saying that this
expression says something indefinable about all
arguments p & q? But the ab-functions must be
introduced as follows: The function p|q is
merely a mechanical instrument for constructing
all possible symbols of ab-functions. The
symbols arising by repeated application of the
symbol "|" do not contain the symbol "p|q". We
need a rule according to which we can form all
symbols of ab-functions, in order to be able to
speak of the class of them; & we now speak of
them e.g. as those symbols of functions which
can be generated by repeated application of the
operation "|". And we say now: For all p´s &
q´s, "p|q" says something indefinable about the
sense of those simple propositions which are
contained in p & q.
Item 201a-1 Recto Page B15
Wittg.- 15
The assertion-sign is logically quite
without significance. It «only» shows, in Frege
& Whitehead & Russell, that these authors hold
the propositions so indicated to be true. """
therefore belongs as little to the proposition
as (say) the number of the proposition. A
proposition cannot possibly assert of itself
that it is true.
Every right theory of judgment must make it
impossible for me to judge that this table
penholders the book. Russell´s theory does not
satisfy this requirement.
It is clear that we understand propositions
without knowing whether they are true or false.
But we can only know the meaning of a
proposition when we know if it is true or false.
What we understand is the sense of the
proposition.
The assumption of the existence of logical
objects makes it appear remarkable that «in the
sciences» propositions of the form "p[or|v]q",
"p⊂q", etc. «are» only then not provisional when
"v" & "⊂" stand within the scope of a
generality-sign [apparent variable].
Item 201a-1 Recto Page B16
Wittg.- 16

4th MS.
If we formed all possible atomic propositions,
the world would be completely described if we
declared the truth or falsehood of each. [I
doubt this.]
The chief characteristic of my theory is
that, in it, p has the same meaning as not-p.
A false theory of relations makes it easily
seem as if the relation of fact & constituent
were the same as that of fact & fact which
follows from it. But the similarity of the two
may be expressed thus: φa.⊂.φ,a a = a.
If a word creates a world so that in it the
principles of logic are true, it thereby creates
a world in which the whole of mathematics holds;
& similarly it could not create a world in which
a proposition was true, without creating its
constituents.
Signs of the form "pv˜p" are senseless, but
not the proposition "(p).p v ˜p". If I know that
this rose is either red or not red, I know
nothing. The same holds of all ab-functions.
To understand a proposition means to know
what is the case if it is true. Hence we can
understand it without knowing if it is true. We
understand it when we understand its
constituents & forms. If we know the meaning of
"a" & "b", & if we know what "xRy" means for all
x´s & y´s, then we also understand "aRb".
I understand the proposition "aRb" when I
know that either the fact that aRb or the fact
that not aRb corresponds to it; but this is not
to be confused with the false opinion that I
understand "aRb" when I know that "aRb or
not-aRb" is the case.
Item 201a-1 Recto Page B17
Wittg.- 17
But the form of a proposition symbolizes in
the following way: Let us consider symbols of
the form "xRy"; to these correspond primarily
pairs of objects, of which one has the name "x",
the other the name "y". The x´s & y´s stand in
various relations to each other, among others
the relation R holds between some, but not
between others. I know now determine the sense
of "xRy" by laying down: when the facts behave
in regard to "xRy" so that the meaning of "x"
stands in the relation R to the meaning of "y",
then I say that they [the facts] are "of like
sense" ["gleichsinnig"] with the proposition
"xRy"; otherwise, "of opposite sense"
[entgegengesetzt"]; I correlate the facts to the
symbol "xRy" by thus dividing them into those of
like sense & those of opposite sense. To this
correlation corresponds the correlation of name
& meaning. Both are psychological. Thus I
understand the form "xRy" when I know that it
discriminates the behaviour of x & y according
as these stand in the relation R or not. In this
way I extract from all possible relations the
relation R, as, by a name, I extract its meaning
from among all possible things.
Strictly speaking, it is incorrect to say:
We understand the proposition p when we know
that ´"p" is true´ = p; for this would naturally
always be the case if accidentally the
propositions to right & left of the symbol "="
were both true or both false. We require not
only an equivalence, but a formal equivalence,
which is bound up with the introduction of the
form of p.
The sense of an ab-function of p is a
function of the sense of p.
Item 201a-1 Recto Page B18
Wittg.- 18
The ab-functions use the discrimination of
facts, which their arguments bring forth, in
order to generate new discriminations.
Only facts can express sense, a class of
names cannot. This is easily shown.
There is no thing which is the form of a
proposition, & no name which is the name of a
form. Accordingly we can also not say that a
relation which in certain cases holds between
things holds sometimes between forms & things.
This goes against Russell´s theory of judgment.
It is «very» easy to forget that, tho´ the
propositions of a form can be either true or
false, each one of these propositions can only
be either true or false, not both.
Among the facts which make "p or q" true,
there are some which make "p & q" true; but the
class which makes "p or q" true is different
from the class which makes "p & q" true; &
«only» this is what matters. For we introduce
this class, as it were, when we introduce
ab-functions.
A very natural objection to the way in
which I have introduced e.g. propositions of the
form xRy is that by it propositions such as
(&Exist;x,y).xRy & similar ones are not explained,
which yet obviously have in common with aRb what
cRd has in common with aRb. But when we
introduced propositions of the form xRy we
mentioned no one particular proposition of this
form; & we only need to introduce (&Exist;x,y).φ(x,y)
for all φ´s in any way which makes the sense of
these propositions dependent on the sense of all
propositions of the form φ(a,b), & thereby the
justification of our procedure is proved.
Item 201a-1 Recto Page B19
Wittg.- 19
The indefinables of logic must be
independent of each other. If an indefinable is
introduced, it must be introduced in all
combinations in which it can occur. We cannot
therefore introduce it first for one
combination, then for another; e.g., if the form
xRy has been introduced, it must henceforth be
understood in propositions of the form aRb just
in the same way as in propositions such as
(&Exist;x,y). xRy & others. We must not introduce it
first for one class of cases, then for the
other; for it would remain doubtful if its
meaning was the same in both cases, & there
would be no ground for using the same manner of
combining symbols in both cases. In short, for
the introduction of indefinable symbols &
classes combinations of symbols the same holds,
mutatis mutandis, that Frege has said for the
introduction of symbols by definitions.
It is a priori likely that the introduction
of atomic propositions is fundamental for the
understanding of all other kinds of
propositions. In fact the understanding of
general propositions obviously depends on that
of atomic propositions.
Cross-definability in the realm of general
propositions leads to the quite similar
questions to those in the realm of ab-functions.
Item 201a-1 Recto Page B20
Wittg.- 20

When we say "A believes p", this sounds, it
is true, as if here we could substitute a proper
name for "p"; but we can see that here a sense,
not a meaning, is concerned, if we say "A
believes that ´p´ is true"; & in order to make
the direction of p even more explicit, we might
say "A believes that ´p´ is true & ´not-p´ is
false". Here the bi-polarity of p is expressed,
& it seems that we shall only be able to express
the proposition "A believes p" correctly by the
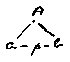
ab-notation; say by making "A" have a relation
to the poles "a" & "b" of a-p-b.

The epistemological questions concerning the
nature of judgment & belief cannot be solved
without a correct apprehension of the form of
the proposition.
The ab-notation shows the dependence of or
& not, & thereby that they are not to be
employed as simultaneous indefinables.
Not: "The complex sign ´aRb´" says that a
stands in the relation R to b; but that ´a´
stands in a certain relation to ´b´ says that
aRb.
In philosophy there are no deductions: it
is purely descriptive.
Philosophy gives no pictures of reality.
Philosophy can neither confirm nor confute
scientific investigation.
Item 201a-1 Recto Page B21
Wittg.- 21
Philosophy consists of logic & metaphysics:
logic is its basis.
Epistemology is the philosophy of
psychology.
Distrust of grammar is the first requisite
for philosophizing.
Propositions can never be indefinables, for
they are always complex. That also words like
"ambulo" are complex appears in the fact that
their root with a different termination gives a
different sense.
Only the doctrine of general indefinables
permits us to understand the nature of
functions. Neglect of this doctrine leads to an
impenetrable thicket.
Philosophy is the doctrine of the logical
form of scientific propositions (not only of
primitive propositions).
The word "philosophy" ought always to
designate something over or under, but not
beside, the natural sciences.
Judgment, «command &» question [&|a]ll
stand on the same level; but all have in common
the propositional form, which does interests us.
The construction structure of the sentence
proposition must be recognized, the rest comes
of itself. But ordinary language conceals the
structure of the proposition: in it, relations
look like predicates, predicates like names,
etc.
Facts cannot be named.
Item 201a-1 Recto Page B22
Wittg.- 22
It is easy to suppose that "individual",
"particular", "complex" etc. are primitive ideas
of logic. Russell e.g. says "individual" &
"matrix" are "primitive ideas". This error
presumably is to be explained by the fact that,
by employment of variables instead of «the»
generality-signs, it comes to seem as if logic
dealt with things which have been deprived of
all properties except thing-hood, & with
propositions deprived of all properties except
complexity. We forget that the indefinables of
symbols [Urbilder von Zeichen] only occur under
the generality-sign, never outside it.
Just as people used to struggle to bring
all propositions into the subject-predicate
form, so now it is natural to conceive every
proposition as expressing a relation, which is
just as incorrect. What is justified in this
desire is fully satisfied by Russell´s theory of
manufactured relations.
One of the most natural attempts at
solution consists in regarding "not-p" as "the
opposite of p", where then "opposite" would be
the indefinable relation. But it is easy to see
that every such attempt to replace the
ab-functions by descriptions must fail.
Item 201a-1 Recto Page B23
Wittg.- 23
The false assumption that propositions are
names leads us to believe that there must be
logical objects: for the meanings of logical
propositions will have to be such things.
A correct explanation of logical
propositions must give them a unique position as
against all other propositions.
No proposition can say anything about
itself, because the symbol of the proposition
cannot be contained in itself; this must be the
basis of the theory of logical types.
Every proposition which says something
indefinable about a thing is a subject-predicate
proposition; every proposition which says
something indefinable about two things expresses
a dual relation between these things, & so on.
Thus every proposition which contains only one
name & one indefinable form is a
subject-predicate proposition, & so on. An
indefinable simple sign symbol can only be a
name, & therefore we can know, by the symbol of
an atomic proposition, whether it is a
subject-predicate proposition.
Item 201a-1 Recto Page B24
Wittg.-

I. Bi-polarity of propositions: sense & meaning,
truth & falsehood.
II. Analysis of atomic propositions: general
indefinables, predicates, etc.
III. Analysis of molecular fu propositions:
ab-functions.
IV. Analysis of general propositions22
[IV|V]. Principles of symbolism: what symbolizes
in a symbol. Facts for facts.
V‹I›. Types
Item 201a-1 Recto Page B25
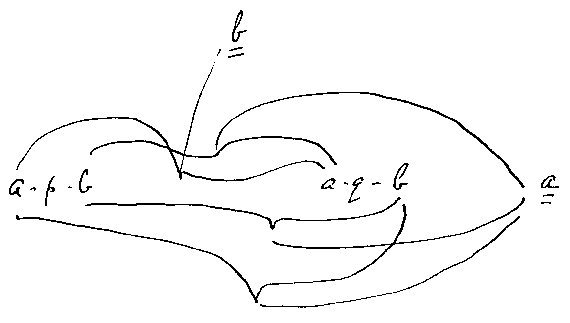
This is the symbol for
˜p v ˜q
Item 201a-1 Recto Page B24