Summary
One reason for thinking the old notation wrong is that it is very unlikely that from every proposition p an infinite number of other propositions not-not-p, not-not-not-not-p, etc., should follow.If only those signs which contain proper names were complex then propositions containing nothing but apparent variables would be simple. Then what about their denials?
The verb of a proposition cannot be „is true” or „is false”, but whatever is true or false must already contain the verb.
Deductions only proceed according to the laws of deduction, but these laws cannot justify the deduction.
One reason for supposing that not all propositions which have more than one argument are relational propositions is that if they were, the relations of judgement and inference would have to hold between an arbitrary number of things.
Every proposition which seems to be about a complex can be analysed into a proposition about its constituents and about the proposition which describes the complex perfectly; i.e., that proposition which is equivalent to saying the complex exists.
The idea that propositions are names of complexes suggests that whatever is not a proper name is a sign for a relation. Because spatial complexes1 consist of Things and Relations only and the idea of a complex is taken from space.
In a proposition convert all its indefinables into variables; there then remains a class of propositions which is not all propositions but a type.

When we say A judges that etc., then we have to mention a whole proposition which A judges. It will not do either to mention only its constituents, or its constituents and form, but not in the proper order. This shows that a proposition itself must occur in the statement that it is judged; however, for instance, „not-p” may be explained. The question „What is negated” must have a meaning.
To understand a proposition p it is not enough to know that p implies ‚„p” is true’, but we must also know that ~p implies „p is false”. This shows the bipolarity of the proposition.
W-F = Wahr-Falsch
To every molecular function a WF scheme corresponds. Therefore we may use the WF scheme itself instead of the function. Now what the WF scheme does is, it correlates the letters W and F with each proposition. These two letters are the poles of atomic propositions. Then the scheme correlates another W and F to these poles. In this notation all that matters is the correlation of the outside poles to the pole of the atomic propositions. Therefore not-not-p is the same symbol as p. And therefore we shall never get two symbols for the same molecular function.
As the ab functions of atomic propositions are bi-polar propositions again we can perform ab operations on them. We shall, by doing so, correlate two new outside poles via the old outside poles to the poles of the atomic propositions.
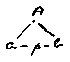
The symbolising fact in a-p-b is that, say2 a is on the left of p and b on the right of p; then the correlation of new poles is to be transitive, so that for instance if a new pole a in whatever way i.e. via whatever poles is correlated to the inside a, the symbol is not changed thereby. It is therefore possible to construct all possible ab functions by performing one ab operation repeatedly, and we can therefore talk of all ab functions as of all those functions which can be obtained by performing this ab operation repeatedly.
[Note by Bertrand Russell]
[NB. ab means the same as WF, which means true-false.]

Naming is like pointing. A function is like a line dividing points of a plane into right and left ones; then „p or not-p” has no meaning because it does not divide the plane.
But though a particular proposition „p or not-p” has no meaning, a general proposition „for all p's, p or not-p” has a meaning because this does not contain the nonsensical function „p or not-p” but the function „p or not-q” just as „for all x's xRx” contains the function „xRy”.

The form of a proposition has meaning in the following way. Consider a symbol „xRy”. To symbols of this form correspond couples of things whose names are respectively „x” and „y”. The things x y stand to one another in all sorts of relations, amongst others some stand in the relation R, and some not; just as I single out a particular thing by a particular name I single out all behaviours of the points x and y with respect to the relation R. I say that if an x stands in the relation R to a y the sign „x R y” is to be called true to the fact and otherwise false. This is a definition of sense.
In my theory p has the same meaning as not-p but opposite sense. The meaning is the fact. The proper theory of judgment must make it impossible to judge nonsense.
It is not strictly true to say that we understand a proposition p if we know that p is equivalent to „p is true” for this would be the case if accidentally both were true or false. What is wanted is the formal equivalence with respect to the forms of the proposition, i.e., all the general indefinables involved. The sense of an ab function of a proposition is a function of its sense. There are only unasserted propositions. ¦ Assertion is merely psychological. In not-p, p is exactly the same as if it stands alone; this point is absolutely fundamental. Among the facts which make „p or q” true there are also facts which make „p and q” true; if propositions have only meaning, we ought, in such a case, to say that these two propositions are identical, but in fact, their sense is different for we have introduced sense by talking of all p's and all q's. Consequently the molecular propositions will only be used in cases where there ab function stands under a generality sign or enters into another function such as „I believe that, etc.,” because then the sense enters.
The ab notation makes it clear that not and or are dependent on one another and we can therefore not use them as simultaneous indefinables. <!> Same objections in the case of apparent variables to old indefinables, as in the case of molecular functions: The application of the ab notation to apparent-variable propositions becomes clear if we consider that, for instance, the proposition „for all x, φx” is to be true when φx is true for all x's and false when jx is false for some x's. We see that some and all occur simultaneously in the proper apparent variable notation.
for (x) φx ; a - (x) - a φ x b - (&Exist; x) - b
and
for (&Exist;x) φ x : a - (&Exist;x) - a φ x b - (x) - b

Old definitions now become tautologous.
In aRb it is not the complex that symbolises but the fact that the symbol a stands in a certain relation to the symbol b. Thus facts are symbolised by facts, or more correctly: that a certain thing is the case in the symbol says that a certain thing is the case in the world.
Judgment, question and command are all on the same level. What interests logic in them is only the unasserted proposition. Facts cannot be named.

A proposition cannot occur in itself. This is the fundamental truth of the theory of types.

Every proposition that says something about one thing is a subject-predicate proposition, and so on.
Therefore we can recognize a subject-predicate proposition if we know it contains only one name and one form, etc. This gives the construction of types. Hence the type of a proposition can be recognized by its symbol alone.

[Components are forms and constituents.]

Take (φ).φ!x. Then if we describe the kind of symbols, for which φ! stands and which, by the above, is enough to determine the type, then automatically „(φ).φ!x” cannot be fitted by this description, because it contains „φ!x” and the description is to describe all that symbolizes in symbols of the φ! - kind. If the description is thus complete vicious circles can just as little occur as for instance in (φ).(x)φ (where (x)φ is a subject-predicate proposition).

First MS.
Indefinables are of two sorts: names, and forms. Propositions cannot consist of names alone; they cannot be classes of names. A name can not only occur in two different propositions, but can occur in the same way in both.
Propositions [which are symbols having reference to facts] are themselves facts: that this inkpot is on this table may express that I sit in this chair.
It can never express the common characteristic of two objects that we designate them by the same name but by two different ways of designation, for, since names are arbitrary, we might also choose different names, and where then would be the common element in the designations? Nevertheless one is always tempted, in a difficulty, to take refuge in different ways of designation.
Frege said „propositions are names”; Russell said „propositions correspond to complexes”. Both are false; and especially false is the statement „propositions are names of complexes”.
It is easy to suppose that only such symbols are complex as contain names of objects, and that accordingly „(&Exist;x,φ).φx” or „(&Exist;x,R,y).xRy” must be simple. It is then natural to call the first of these the name of a form, the second the name of a relation. But in that case what is the meaning of (e.g.) „˜(&Exist;x,y).xRy”? Can we put „not” before a name?
There are positive and negative facts: if the proposition „this rose is not red” is true, then what it signifies is negative. But the occurrence of the word „not” does not indicate this unless we know that the signification of the proposition „this rose is red” (when it is true) is positive. It is only from both, the negation and the negated proposition, that we can conclude to a characteristic of the significance of the whole proposition. (We are not here speaking of negations of general propositions, i.e. of such as contain apparent variables. Negative facts only justify the negations of atomic propositions.)
Positive and negative facts there are, but not true and false facts.
If we overlook the fact that propositions have a sense which is independent of their truth or falsehood, it easily seems as if true and false were two equally justified relations between the sign and what is signified. (We might then say e.g. that „q” signifies in the true way what „not-q” signifies in the false way). But are not true and false in fact equally justified? Could we not express ourselves by means of false propositions just as well as hitherto with true ones, so long as we know that they are meant falsely? ¦ No! For a proposition is then true when it is as we assert in this proposition; and accordingly if by „q” we mean „not-q”, and it is as we mean to assert, then in the new interpretation „q” is actually true and not false. But it is important that we can mean the same by „q” as by „not-q”, for it shows that neither to the symbol „not” nor to the manner of its combination with „q” does a characteristic of the denotation of „q” correspond.

2nd MS.
We must be able to understand propositions which we have never heard before. But every proposition is a new symbol. Hence we must have general indefinable symbols; these are unavoidable if propositions are not all indefinable.
Whatever corresponds in reality to compound propositions must not be more than what corresponds to their several atomic propositions.
Not only must logic not deal with [particular] things, but just as little with relations and predicates.
There are no propositions containing real variables.
What corresponds in reality to a proposition depends upon whether it is true or false. But we must be able to understand a proposition without knowing if it is true or false.
What we know when we understand a proposition is this: We know what is the case if the proposition is true, and what is the case if it is false. But we do not know [necessarily] whether it is true or false.
Propositions are not names.
We can never distinguish one logical type from another by attributing a property to members of the one which we deny to members of the other.
Symbols are not what they seem to be. In „aRb”, „R” looks like a substantive, but is not one. What symbolizes in „aRb” is that R occurs between a and b. Hence „R” is not the indefinable in „aRb”. Similarly in „φx”, „φ” looks like a substantive but is not one; in „˜p”, „˜” looks like „φ” but is not like it. This is the first thing that indicates that there may not be logical constants. A reason against them is the generality of logic: logic cannot treat a special set of things.
All that is essential about molecular functions is their T-F schema [i.e. the statement of the cases when they are true and the cases when they are false].
Alternative indefinability shows that the indefinables have not been reached.
Every proposition is essentially true-false: to understand it, we must know both what must be the case if it is true, and what must be the case if it is false. Thus a proposition has two poles, corresponding to the case of its truth and the case of its falsehood. We call this the sense of a proposition.
In regard to notation, it is important to note that not every feature of a symbol symbolizes. In two molecular functions which have the same T-F schema, what symbolizes must be the same. In „not-not-p”, „not-p” does not occur; for „not-not-p” is the same as ”p”, and therefore, if „not-p” occurred in „not-not-p”, it would occur in „p”.
Logical indefinables cannot be predicates or relations, because propositions, owing to sense, cannot have predicates or relations. Nor are „not” and „or”, like judgment, analogous to predicates or relations, because they do not introduce anything new.
Propositions are always complex even if they contain no names.
„a” is indefinable;
„b” is indefinable;
Whatever „x” and „y” may mean, „xRy” says something indefinable about their meanings.
A complex symbol must never be introduced as a single indefinable. (Thus e.g. no proposition is indefinable.) For if one of its parts occurs also in another connection, it must there be re-introduced. And would it then mean the same?
The ways by which we introduce our indefinables must permit us to construct all propositions that have sense from these indefinables alone. It is easy to introduce „all” and „some” in a way that will make the construction of (say) „(x,y).xRy” possible from „all” and „xRy” as introduced before.

3rd MS.
An analogy for the theory of truth: Consider a black patch on white paper; then we can describe the form of the patch by mentioning, for each point of the surface, whether it is white or black. To the fact that a point is black corresponds a positive fact, to the fact that a point is white (not black) corresponds a negative fact. If I designate a point of the surface (one of Frege's „truth-values”), this is as if I set up an assumption to be decided upon. But in order to be able to say of a point that it is black or that it is white, I must first know when a point is to be called black and when it is to be called white. In order to be able to say that „p” is true (or false), I must first have determined under what circumstances I call a proposition true, and thereby I determine the sense of a proposition. The point in which the analogy fails is this: I can indicate a point of the paper that is white and black, but to a proposition without sense nothing corresponds, for it does not designate a thing (truth-value), whose properties might be called „false” or „true”; the verb of a proposition is not „is true” or „is false”, as Frege believes, but what is true must already contain the verb.
The comparison of language and reality is like that of retinal image and visual image: to the blind spot nothing in the visual image seems to correspond, and thereby the boundaries of the blind spot determine the visual image - as true negations of atomic propositions determine reality.
Those symbols which are called propositions in which „variables occur” are in reality not propositions at all, but only schemes of propositions, which only become propositions when we replace the variables by constants. There is no proposition which is expressed by „x = x”, for „x” has no signification; but there is a proposition „(x).x = x” and propositions such as „Socrates = Socrates” etc.
In books on logic, no variables ought to occur, but only the general propositions which justify the use of variables. It follows that the so-called definitions of logic are not definitions, but only schemes of definitions, and instead of these we ought to put general propositions; and similarly the so-called primitive ideas (Urzeichen) of logic are not primitive ideas, but the schemes of them. The mistaken idea that there are things called facts or complexes and relations easily leads to the opinion that there must be a relation of questioning to the facts, and then the question arises whether a relation can hold between an arbitrary number of things, since a fact can follow from arbitrary cases. It is a fact that the proposition which e.g. expresses that q follows from p and p⊂q is this: p.p⊂q.⊂p.q.q.
Russell's „complexes” were to have the useful property of being compounded, and were to combine with this the agreeable property that they could be treated like „simples”. But this alone made them unserviceable as logical types, since there would have been significance in asserting, of a simple, that it was complex. But a property cannot be a logical type.
Every statement about apparent complexes can be resolved into the logical sum of a statement about the constituents and a statement about the proposition which describes the complex completely. How, in each case, the resolution is to be made, is an important question, but its answer is not unconditionally necessary for the construction of logic.
If we change a constituent a of a proposition φ(a) into a variable, then there is a class
˜p {(&Exist;x).φ(x) = p}.
This class in general still depends upon what, by an arbitrary convention, we mean by „j(x)”. But if we change into variables all those symbols whose significance was arbitrarily determined, there is still such a class. But this is now not dependent upon any convention, but only upon the nature of the symbol „j(x)”. It corresponds to a logical type.
Types can never be distinguished from each other by saying (as is often done) that one has these but the other has that properties, for this presupposes that there is a meaning in asserting all these properties of both types. But from this it follows that, at best, these properties may be types, but certainly not the objects of which they are asserted.
The very possibility of Frege's explanations of „not-p” and „if p then q”, from which it follows that not-not-p denotes the same as p, makes it probable that there is some method of designation in which „not-not-p” corresponds to the same symbol as „p”. But if this method of designation suffices for logic, it must be the right one.
Names are points, propositions arrows - they have sense. The sense of a proposition is determined by the two poles true and false. The form of a proposition is like a straight line, which divides all points of a plane into right and left. The line does this automatically, the form of proposition only by convention.
In place of every proposition „p”, let us write „abp”. Let every correlation of propositions to each other or of names to propositions be effected by a correlation of their poles „a” and „b”. Let this correlation be transitive. Then accordingly „a-ab-bp” is the same symbol as „abp”. Let n propositions be given. I then call a „class of poles” of these propositions every class of n members, of which each is a pole of one of the n propositions, so that one member corresponds to each proposition. I then correlate with each class of poles one of two poles (a and b). The sense of the symbolizing fact thus constructed I cannot define, but I know it.
If p = not-not-p etc., this shows that the traditional method of symbolism is wrong, since it allows a plurality of symbols with the same sense; and thence it follows that, in analyzing such propositions, we must not be guided by Russell's method of symbolizing.
Neither the sense nor the meaning of a proposition is a thing. These words are incomplete symbols.
It is impossible to dispense with propositions in which the same argument occurs in different positions. It is obviously useless to replace φ(a,a) by φ(a,b).a = b.
Since the ab-functions of p are again bi-polar propositions, we can form ab-functions of them, and so on. In this way a series of propositions will arise, in which in general the symbolizing facts will be the same in several members. If now we find an ab-function of such a kind that by repeated application of it every ab-function can be generated, then we can introduce the totality of ab-functions as the totality of those that are generated by application of this function. Such a function is ˜pv˜q.

Every right theory of judgment must make it impossible for me to judge that this table penholders the book. Russell's theory does not satisfy this requirement.
It is clear that we understand propositions without knowing whether they are true or false. But we can only know the meaning of a proposition when we know if it is true or false. What we understand is the sense of the proposition.
The assumption of the existence of logical objects makes it appear remarkable that in the sciences propositions of the form „pvq”, „p⊃q”, etc. are only then not provisional when „v” and ”⊃” stand within the scope of a generality-sign [apparent variable].

4th MS.
If we formed all possible atomic propositions, the world would be completely described if we declared the truth or falsehood of each. [I doubt this.]
The chief characteristic of my theory is that, in it, p has the same meaning as not-p.
A false theory of relations makes it easily seem as if the relation of fact and constituent were the same as that of fact and fact which follows from it. But the similarity of the two may be expressed thus: φa.⊃.φ,a a = a.
If a word creates a world so that in it the principles of logic are true, it thereby creates a world in which the whole of mathematics holds; and similarly it could not create a world in which a proposition was true, without creating its constituents.
Signs of the form „pv˜p” are senseless, but not the proposition „(p).p v ˜p”. If I know that this rose is either red or not red, I know nothing. The same holds of all ab-functions.
To understand a proposition means to know what is the case if it is true. Hence we can understand it without knowing if it is true. We understand it when we understand its constituents and forms. If we know the meaning of „a” and „b”, and if we know what „xRy” means for all x's and y's, then we also understand „aRb”.
I understand the proposition „aRb” when I know that either the fact that aRb or the fact that not aRb corresponds to it; but this is not to be confused with the false opinion that I understand „aRb” when I know that „aRb or not-aRb” is the case.
Strictly speaking, it is incorrect to say: We understand the proposition p when we know that ‚„p” is true’ = p; for this would naturally always be the case if accidentally the propositions to right and left of the symbol „=” were both true or both false. We require not only an equivalence, but a formal equivalence, which is bound up with the introduction of the form of p.
The sense of an ab-function of p is a function of the sense of p.
Only facts can express sense, a class of names cannot. This is easily shown.
There is no thing which is the form of a proposition, and no name which is the name of a form. Accordingly we can also not say that a relation which in certain cases holds between things holds sometimes between forms and things. This goes against Russell's theory of judgment.
It is very easy to forget that, tho. the propositions of a form can be either true or false, each one of these propositions can only be either true or false, not both.
Among the facts which make „p or q” true, there are some which make „p and q” true; but the class which makes „p or q” true is different from the class which makes „p and q” true; and only this is what matters. For we introduce this class, as it were, when we introduce ab-functions.
A very natural objection to the way in which I have introduced e.g. propositions of the form xRy is that by it propositions such as (&Exist;x,y).xRy and similar ones are not explained, which yet obviously have in common with aRb what cRd has in common with aRb. But when we introduced propositions of the form xRy we mentioned no one particular proposition of this form; and we only need to introduce (&Exist;x,y).φ(x,y) for all φ's in any way which makes the sense of these propositions dependent on the sense of all propositions of the form φ(a,b), and thereby the justification of our procedure is proved.
It is a priori likely that the introduction of atomic propositions is fundamental for the understanding of all other kinds of propositions. In fact the understanding of general propositions obviously depends on that of atomic propositions.
Cross-definability in the realm of general propositions leads to the quite similar questions to those in the realm of ab-functions.


The epistemological questions concerning the nature of judgment and belief cannot be solved without a correct apprehension of the form of the proposition.
The ab-notation shows the dependence of or and not, and thereby that they are not to be employed as simultaneous indefinables.
Not: „The complex sign ‚aRb’” says that a stands in the relation R to b; but that ‚a’ stands in a certain relation to ‚b’ says that aRb.
In philosophy there are no deductions: it is purely descriptive.
Philosophy gives no pictures of reality.
Philosophy can neither confirm nor confute scientific investigation.
Epistemology is the philosophy of psychology.
Distrust of grammar is the first requisite for philosophizing.
Propositions can never be indefinables, for they are always complex. That also words like „ambulo” are complex appears in the fact that their root with a different termination gives a different sense.
Only the doctrine of general indefinables permits us to understand the nature of functions. Neglect of this doctrine leads to an impenetrable thicket.
Philosophy is the doctrine of the logical form of scientific propositions (not only of primitive propositions).
The word „philosophy” ought always to designate something over or under, but not beside, the natural sciences.
Judgment, command and question all stand on the same level; but all have in common the propositional form, which does interests us.
The structure of the proposition must be recognized, the rest comes of itself. But ordinary language conceals the structure of the proposition: in it, relations look like predicates, predicates like names, etc.
Facts cannot be named.
Just as people used to struggle to bring all propositions into the subject-predicate form, so now it is natural to conceive every proposition as expressing a relation, which is just as incorrect. What is justified in this desire is fully satisfied by Russell's theory of manufactured relations.
One of the most natural attempts at solution consists in regarding „not-p” as „the opposite of p”, where then „opposite” would be the indefinable relation. But it is easy to see that every such attempt to replace the ab-functions by descriptions must fail.
A correct explanation of logical propositions must give them a unique position as against all other propositions.
No proposition can say anything about itself, because the symbol of the proposition cannot be contained in itself; this must be the basis of the theory of logical types.
Every proposition which says something indefinable about a thing is a subject-predicate proposition; every proposition which says something indefinable about two things expresses a dual relation between these things, and so on. Thus every proposition which contains only one name and one indefinable form is a subject-predicate proposition, and so on. An indefinable simple symbol can only be a name, and therefore we can know, by the symbol of an atomic proposition, whether it is a subject-predicate proposition.

II. Analysis of atomic propositions: general indefinables, predicates, etc.
III. Analysis of molecular propositions: ab-functions.
IV. Analysis of general propositions.
V. Principles of symbolism: what symbolizes in a symbol. Facts for facts.
VI. Types.
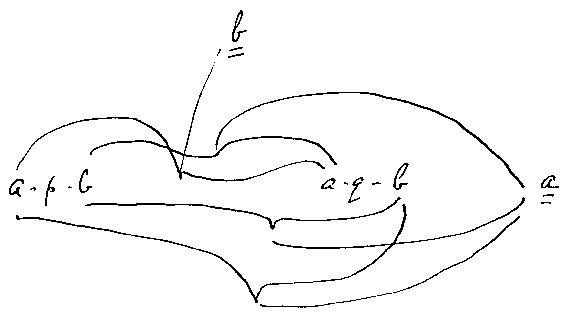
This is the symbol for
˜p v ˜q