From the ALWS archives: A selection of papers from the International Wittgenstein Symposia in Kirchberg am Wechsel

1. Überblick

Der vorliegende Beitrag versucht die zentralen Elemente der Ontologie und Erkenntnistheorie Wittgensteins an einer in der logikorientierten Programmiersprache PROLOG konstruierten Modell-Welt zu exemplifizieren, so dass einerseits die universelle Anwendbarkeit der ontologischen Kategorien "Sachverhalt", "Tatsache", "Ding", "Welt" und "Substanz" und andererseits die Funktion der "Abbildtheorie der Satzbedeutung" bei der Modellierung von Wirklichkeitsfragmenten in PROLOG deutlich wird. Die Gesamtheit der Tatsachen der Modell-Welt wird als Sammlung von Fakten und regeln in der Datenbank repräsentiert; die Sprache, in der Anfragen an die Datenbank formuliert werden, ist eine in PROLOG definierte - um Frageoperatoren erweiterte - PL-Sprache, deren Formeln im Rahmen einer Interpretationssemantik anhand der Datenbankinformationen ausgewertet werden. Das für die Auswertung der Formeln benutzte Unifikatonsverfahren lässt sich - grob gesagt - als Explikation der Abbildtheorie der Satzbedeutung verstehen, insofern es auf der "Überdeckung" von Anfragen (Sätzen) und Fakten (Tatsachen) basiert. Die Modell-Welt genügt ferner den Anforderungen des logischen Atomismus, der die Möglichkeit des Aufbaus der Welt aus logisch einfachsten, von einander unabhängigen Elementen postuliert. Die einfachsten Elemente der Modell-Welt sind die Relationen "ist direkter Teil von", "ist Attribut von" und "befindet sich an", aus denen sich u.a. rekursiv weitere Relationen ableiten lassen, sowie die "algebraischen Atome" der in Verbänden organisierten Individuen der Grundfarben, Vierecke und Gebäudeteile, die den Baukasten der Modell-Welt bilden. Das Beispiel der Modell-Welt zeigt, dass unter idealen Umständen die Tractatus-Philosophie eine plausible und zwanglose Entsprechung in Datenbanksystemen und ihrer Sprache findet. Aufgrund der gebotenen Kürze vermeidet der Beitrag technische Details zugunsten einer mehr umgangssprachlichen Skizze des gesamten Projektes¹.

2. Logische Modellierung

Der erste Schritt des Vorhabens besteht zunächst darin, eine Modell-Welt aus wohldefinierten Elementen wie z.B. Farben, Formen und Dingen mittels weniger Grundrelationen systematisch aufzubauen und alle Fakten dieser Modell-Welt in einer Datenbank zu sammeln. Die Datenbank enthält dann das sämtliches Wissen über die Modell-Welt. An die Fakten der Datenbank können Anfragen in Form von prädikatenlogischen Formeln, die um Frageoperatoren erweitert sind, gestellt werden. Die Modell-Welt erkauft ihre logische Transparenz und Vollständigkeit durch ein hohes Maß an Einfachheit, aber in ihrer Beispielhaftigkeit verweist sie auf die Möglichkeit, anspruchsvollere Wissensfragmente, die z.B. auf chemischen, biologischen oder medizinischen Klassifikationen beruhen, zu rekonstruieren.

Zunächst zur Datenbank. Der hier eingesetzte Typ von Datenbank ist eine sogenannte relationale Datenbank. Eine relationale Datenbank besteht aus einer Menge von Individuenbezeichnungen D, dem sogenannten Wertebereich, und einer Menge von Relationsbezeichnungen R. Die Individuen sind in meinem Programm die Grundfarben wie z.B. Rot oder Grün, Vierecks-Formen wie z.B. Quadrat oder Trapez und Gebäudeteil wie z.B. Wand oder Fenster. Die Relationen drücken die Beziehungen zwischen den Individuen aus; die Grundrelationen, aus denen weitere abgeleitet werden, sind: "ist direkter Teil von", "ist Attribut von" und "befindet sich an". Typische Fakten der Datenbank sind:

• DIR_TEIL (GRUEN, GELB).
• DIR_TEIL (TRAPEZ, QUADRAT).
• DIR_TEIL (DACH, HAUS).
• ...
• ATTRIBUT(ROT, WAND).
• ATTRIBUT(QUADRAT, FENSTER).
• ...
• AN (SCHLOT, DACH).
• ...

Die Fakten der Datenbank sind die wahren Sachverhalte (Tatsachen); die nicht in der Datenbank aufgeführten Fakten sind die falschen Sachverhalte. Die Menge der wahren und falschen Sachverhalte der Datenbank heißt Interpretation für die noch zu definierende prädikatenlogische Sprache².

Schritt 1:

    Die drei Individuenbereiche der Farben, Formen und Dingen werden durch die Relation "ist direkter Teil von" - d.h. größter echter Teil von (covering relation) organisiert und als Fakten in die Datenbank abgelegt. Auf diese Weise erhält man zwei boolesche Verbände, die der Farben und Vierecke, und einen Supremum-Halbverband der Gebäudeteile. Die Verbandsstruktur motiviert ein Vollständigkeitskriterium für die Partition der Individuenbereiche. Die Verbandsstruktur lässt sich - für kleine Mengen grafisch darstellen. Hier der boolesche Verband der Grundfarben:

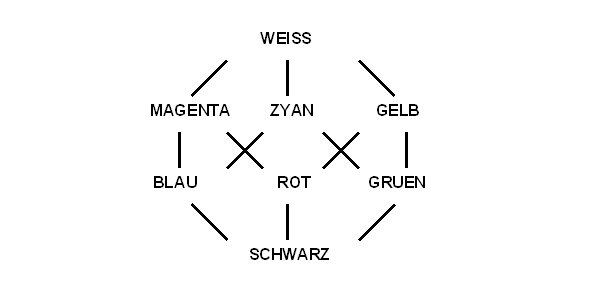
Innerhalb eines Verbandes sind die Atome, hier Rot, Grün und Blau, als einfachste Elemente strukturell ausgezeichnet; ebenso lasse sich der Eins-Teil Weiß, der Null-Teil Schwarz und die Sub-Atome Magenta, Zyan und Gelb strukturell kennzeichnen. Ähnlich wie der Farb-Verband strukturieren sich der Verband der Vierecke und der Verband der Gebäudeteile.

Schritt 2:

    Die so mittels der Relationen "ist direkter Teil von" in algebraischen Verbänden organisierten Elemente der Farben, Vierecke und Gebäudeteile sind sozusagen der Baukasten für unsere Modell-Welt. Wir entscheiden uns aus Gründen der Anschaulichkeit für folgende simple Kombination der Elemente, die ein Haus mit einer beistehenden Fahne zeigt; aber natürlich sind weitaus reichhaltigere Arrangements möglich.

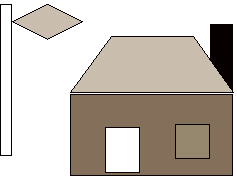
Sämtliche Fakten dieser Modell-Welt werden des weiteren durch die Relationen "ist Attribut von" und "befindet sich an" formuliert und in die Datenbank abgelegt.

Schritt 3:

    Aus den Grundelementen lassen sich weitere Relationen ableiten, wodurch gezieltere und interessantere Anfragen an die Datenbank möglich werden, als dies bei der Beschränkung auf die Grundrelationen der Fall wäre. Die abgeleiteten Relationen bilden den ersten Teil der Regelmenge; den zweiten Teil bilden jene Regeln, die die Logiksprache der Anfragen definieren. Die Regelmengen werden der Datenbank hinzugefügt. Fakten und Regeln zusammen werden auch als Axiome bezeichnet, da sie als wahr gesetzt sind. Zunächst zu den abgeleiteten Relationen:

Die Ableitung von speziellen Relationen aus Grundrelationen ist in PROLOG relativ einfach, was an einigen algebraischen Operationen auf Relationen verdeutlicht werden soll:

1. Projektion der zweiten auf die erste Relation:
   P(X) :- Q(X,Y).
2. Kartesisches Produkt von zwei Relationen:
   P(X,Y) :- Q(X), R(X).
3. Vereinigung von Q und R auf der ersten Relation:
   P(X,Y) :- Q(Z,X), R(Z,Y).

Aus den oben genannten Grundrelationen lassen sich weitere Relationen ableiten, die das Teil-Ganzes-Verhältnis weiter spezifizieren. Abgeleitete Relationen sind z.B.:

• TEIL(X,Y)                                                              x ist Teil von y
• ECHTER_TEIL(X,Y)                                                  x ist echter Teil von y
• NULL_TEIL(X,Y)                                                      x ist Null-Teil von y
• EINS_TEIL(X,Y)                                                      x ist Eins-Teil von y
• ATOM_TEIL(X,Y)                                                     x ist atomarer Teil von y
• STUECK(X,Y)                                                          x ist Stück von y
• ATTRIBUT_TEIL(X,Y)                                               x ist attributiver Teil von y
• MOMENT(X,Y)                                                         x ist Moment von y
• VERBUNDEN(X,Y)                                                    x ist mit y verbunden
• AEHNLICH (X,Y)                                                      x ist ähnlich mit y
• ...

Am Beispiel der abgeleiteten Relation "ist echter Teil von" lässt sich das für die logische Programmierung typische Verfahren der rekursiven Definition zeigen:

• ECHTER_TEIL(X,Y) :-                                              (Abbruchbedingung)
• DIR_TEIL(X,Y).
• ECHTER_TEIL(X,Y):-                                               (Rekursionsbedingung)
• DIR_TEIL(X,Z), ECHTER_TEIL(Z,Y).

Das heißt: Echte Teile sind die direkten Teile von X und die echten Teile der direkten Teile von X. Der Begriff "echter Teil" wird also durch sich selbst erklärt. Dass dies keine unsinnige Definitionsweise ist, erkennt man am besten, wenn man sie prozedural betrachtet:

    "Wenn du einen echten Teil von X suchst, so suche zunächst die direkten Teile von X. Wenn du noch weiter suchen sollst, suche einen echten Teil des direkten Teils und von diesem einen echten Teil."

Schritt 4:

    Die Anfragen an die Modell-Welt werden durch Auswertung prädikatenlogischer Formeln beantwortet. Daher ist im Anschluss an die Teil-Ganzes-Regeln ein Regelapparat zu konstruieren, der die Syntax und Semantik prädikatenlogischer Formeln definiert. Der Aufbau der prädikatenlogischen Syntax und Semantik in PROLOG ist die eigentliche programmiertechnische und systematische Leistung, die im Rahmen dieses Beitrages unmöglich nachvollzogen werden kann. Der Interessierte sei auf den Programmtext verwiesen. Hier nur soviel: Das Programm errechnet aus der Interpretation atomarer Formeln den Wert komplexer Formeln. Diese Berechnung kann aufgrund der begrenzten Fakten intuitiv im Rahmen einer Interpretationssemantik leicht nachvollzogen werden. Die komplexen Formeln entstehen aus den atomaren Formeln durch die Verknüpfung mittels Junktoren (nicht, und, oder, wenn-dann), Quantoren (existiert, alle) und Frageoperatoren (welche). Die Funktionsweise dieser sprachlichen Elemente macht den Kern der prädikatenlogisch formulierten Anfragen aus. Hier einige Beispiele aus dem Dialog mit der Modell-Welt:

• Typ 1: Ja-Nein-Fragen
• Umschreibung:
  Ist die Aussage "Die Tür ist grün." Wahr? Ja.
• PROLOG:
  ?- ANTWORT(JA-NEIN(ATTRIBUT(TUER,GRUEN)),ANTWORT).
• ANTWORT = JA
  
• Typ 2: Welche-Fragen
• Umschreibung:
  Welche rechteckigen Gegenstände sind mit dem Schlot verbunden? Das sind die Mauer und die Tür.
• PROLOG:
  ?- ANTWORT (WELCHE(X,UND(VERBUNDEN(X,SCHLOT),ATTRIBUT(RECHTECK,X)))), ANTWORT).
  X = MAUER;
  ANTWORT = MAUER;
  X = TUER
  ANTWORT = TUER.
  
• Typ 3: Wahr-Falsch-Fragen
• Umschreibung:
  Ist die Aussage wahr: Gibt es ein X für alle Y, so dass gilt: Wenn Y ein Moment eines Rechtecks ist, dann ist X ein echter Teil von Y? Die Aussage ist wahr.
• PROLOG:
  ?- SEM_WERT(EXISTIERT(X,FUER_ALLE(Y, WENN(MOMENT(Y,RECHTECK), ECHTER_TEIL(X,Y)))),WERT).
  WERT = WAHR

3. Anwendungen auf Wittgensteins "Tractatus"

Die oben konstruierte Modell-Welt gibt uns einen Schlüssel für die Interpretation von Wittgensteins "Tractatus" an die Hand. Dies ist gewiss kein Zufall, da sich die Tractatus-Ontologie eng an der Konzeption einer logischen Idealsprache orientiert und die kategorialen Formen der Welt durch die Kategorien dieser Idealsprache bestimmt sein lässt. Die wichtigsten Begriffe des ontologischen Grundgerüstes - Sachverhalt, Tatsache, Ding, Welt und Substanz - lassen sich zwanglos an der Struktur der Modell-Welt erläutern.

Die fundamentale Unterscheidung innerhalb der Kategorien, die Wittgenstein im "Tractatus" vornimmt, ist die zwischen der Kategorie der Tatsachen und die der Nicht-Tatsachen. Die Kategorie der Nicht-Tatsachen wird kategorial unterschieden in Einzeldinge und Attribute, und letztere werden wiederum unterschieden in Eigenschaften und Relationen. Im ersten Satz des "Tractatus": "Die Welt ist alles, was der Fall ist.", sowie im darauf folgenden Erläuterungssatz 1.1: "Die Welt ist die Gesamtheit der Tatsachen, nicht der Dinge." wird die Welt zur Kategorie der Tatsachen gerechnet. In Hinblick auf die Modell-Welt ist diese Aussage unmittelbar plausibel, da die Modell-Welt durch die Menge aller gültigen Fakten (Tatsachen) der Datenbank bestimmt ist. Tatsachen sind zu unterscheiden von dem, was Wittgenstein Sachverhalte nennt. Während eine Tatsache stets etwas betrifft, was der Fall ist, stellt ein Sachverhalt bloß etwas dar, was möglicherweise der Fall ist. Dementsprechend gehören die möglichen Fakten, die nicht explizit in die Datenbank aufgenommen worden sind, zu den Sachverhalten. Anders gesagt: Jene Anfragen (im Rahmen der definierten Elemente) an die Datenbank, die PROLOG-Interpreter negativ beantwortet, beziehen sich auf Sachverhalte, jene, die er positiv beantwortet, auf Tatsachen.

Sowohl Sachverhalte als auch Tatsachen können atomar oder komplex sein. Die atomaren Sachverhalte bzw. Tatsachen sind etwas "logisch Einfaches", das nicht selbst wieder in einfachere Sachverhalte zerfällt, sondern sich in Einzeldinge und Attribute gliedert. Die Fakten der Datenbank, die Attribute von bzw. Relationen zwischen Einzeldingen definieren, sind demnach atomare Tatsachen, und alle potentiellen Fakten sind atomare Sachverhalte. Komplexe Tatsachen bzw. Sachverhalte sind jene, die durch logische Operationen auf atomare zurückgeführt werden können. Man betrachte beispielsweise die PROLOG-Anfrage:

• ?- SEM_WERT (UND(TEIL(DACH,HAUS), TEIL(FENSTER,HAUS)), WERT).

Dann ist klar, dass sie sich auf einen komplexen Sachverhalt richtet, da die Relation "ist Teil von" auf "ist direkter Teil von" und die Gültigkeit der mit "und" verknüpften Aussagen auf die Gültigkeit der beiden Teilaussagen zurückführbar ist. Ferner ist "Dach" innerhalb des Supremum-Halbverbandes der Gebäudeteile auf die Kombination "Schlot" und "Eindeckung" zurückzuführen etc. Wie das Beispiel zeigt, verdankt sich die Komplexität der Aussage nicht allein ihrer wahrheitsfunktionalen Zusammensetzung, sondern ebenso dem Vorhandensein einer komplexen Relation zwischen komplexen Einzeldingen. Hier erhebt sich die Frage nach den empirischen Anteilen bei der Organisation von Teil-Ganzes-Verbänden, die die Auffassung von rein logisch kombinierbaren Einzeldingen zweifelhaft erscheinen lassen. Beispielsweise beruht die Bildung des Supremums von "Rot" und "Blau" auf der additiven Mischung und nicht auf einer logischen Kombinations-Operation.

Von den atomaren Sachverhalten sagt Wittgenstein, dass sie voneinander unabhängig seien (2.061). Damit ist gemeint, wenn A und B atomare Sachverhalte sind, so gibt es vier Möglichkeiten des Bestehens und Nicht-Bestehens: A und B können als Fakten in der Datenbank auftreten, oder nur A, oder nur B, oder weder A noch B. Damit sind alle möglichen Welten durch alle möglichen Teilmengen aus der Menge der atomaren Sachverhalte gegeben, und nur eine der möglichen Welten ist als die wirkliche Welt ausgezeichnet. Beispielsweise könnte man neben der Datenbank der Modell-Welt weitere "mögliche Datenbanken" definieren, die in ihrer Gesamtheit alle möglichen Modell-Welten bestimmen. Allerdings sind an dieser Stelle weitere Spezifizierungen hinsichtlich des durch die Sachverhalte aufgespannten logischen Raumes nötig, die hier übergangen werden müssen.

Nach 2.01 ist ein (atomarer) Sachverhalt eine Verbindung von Dingen oder Gegenständen. "Ding" bzw. "Gegenstand" bezeichnet hier etwas anderes als "Einzelding"; denn die Verbindung von Einzeldingen enthält mindestens ein Attribut bzw. eine Relation. Dinge umfassen also Einzeldinge und Relationen. Jetzt wird es möglich, einen Zugang zu finden zu dem Satz 2.021: "Die Gegenstände bilden die Substanz." Es handelt sich hierbei um die Einzeldinge und Relationen, die alle möglichen Sachverhalte konstituieren und daher die "unveränderlichen" Bausteine (Substanz) aller möglichen Welten bilden. In der Modell-Welt ist die Substanz der Welt eindeutig bestimmt durch die Relationen "ist direkter Teil von", "ist attributiver Teil von" und "befindet sich an" sowie durch die Individuen der Farben, Vierecke und Gebäudeteile. Insbesondere wird dem Gedanken des logischen Atomismus dadurch entsprochen, dass die Individuen wiederum aus letzten Atomen, nämlich den algebraischen Atomen der jeweiligen Verbandsstruktur - z.B. den Urfarben Rot, Grün, Blau - konstituiert werden können. Damit ist der Nachweis erbracht, dass sich zumindest einige der ontologischen Grundgedanken des "Tractatus", den "logischen Atomismus" betreffen, an der Modell-Welt illustrieren lassen. Ob sich der Atomismus in anspruchsvollere Fragmente der Wirklichkeit transferieren lässt, bleibt allerdings fraglich.

In Satz 2.1. wechselt Wittgenstein von der ontologischen zur erkenntnistheoretischen Ebene. Es heißt dort, dass wir uns Bilder der Tatsachen machen. Bilder sind hier nicht in einem naturalistischen Sinne zu verstehen, sondern vielmehr als komplexe Relationen.³ Es handelt sich bei Bildern ebenfalls um Tatsachen und nicht um Dinge, wie der Satz 2.141 sagt: "Das Bild ist eine Tatsache." Damit etwas ein Bild einer Tatsache ist, muss es die Voraussetzung erfüllen, dass es dieselbe innere Struktur besitzt wie die abzubildende Tatsache. Das heißt, es müssen Elemente von gleicher Zahl und Kategorie zur Verfügung stehen und es muss einen Isomorphismus zwischen den beiden komplexen Tatsachen geben. Für einen derartigen Isomorphismus zwischen zwei Tatsachen T₁ und T₂ ist erforderlich:

1. Es muss eine umkehrbar eindeutige Zuordnung zwischen den Individuen und gleichstelligen Attributen von T₁ und T₂ geben, und
2. auf der Grundlage einer solchen Zuordnung zwischen kategorial gleichen Elementen von T₁ und T2 muss es eine umkehrbar eindeutige Zuordnung zwischen den einfachen Sachverhalten T₁ und T₂ geben, so dass ein Sachverhalt in T₁ genau dann besteht, wenn der aufgrund dieser Zuordnung entsprechende Sachverhalt von T₂ existiert.

Zwei in diesem Sinne isomorphe Tatsachen lassen sich als Bilder von einander auffassen. Ist die Bedingung 1. erfüllt, aber nicht 2., d.h. ist die kategoriale Gleichheit ohne Isomorphie erfüllt, so spricht Wittgenstein von einem "falschen Bild", sind hingegen 1. und 2. erfüllt, von einem "wahren Bild". Wittgenstein lehnt jeden synthetischen Apriorismus ab: "Aus dem Bild allein ist nicht zu erkennen, ob es wahr oder falsch ist." (Satz 2.224) und "Ein a priori wahres Bild gibt es nicht." (Satz 2.225) Ob ein Bild wahr ist hängt davon ab, ob die ihm zugeordnete Tatsache existiert, d.h. ein Bild stellt eine Tatsache dar, ein falsches Bild nur einen möglichen Sachverhalt.. Ein wahrer Satz ist isomorph zu der durch ihn dargestellten Tatsache, ein falscher Satz ist nicht isomorph in diesem Sinne, aber doch isomorph zu einem möglichen Sachverhalt. Die wichtigste Anwendung des Bildbegriffs findet sich in der Theorie der Satzbedeutung. Nach 4.01 ist der Satz ein "Bild der Wirklichkeit". Die Klärung dieser Aussage setzt voraus, dass zwei Arten von Sätzen unterschieden werden können: komplexe Sätze, die logische Ausdrücke wie Junktoren enthalten, und einfache Sätze, die behaupten. Dass zwischen Dingen eine bestimmte Relation besteht, oder ein Ding eine bestimmte Eigenschaft hat. Die Tatsache, dass die Tür grün ist, kann z.B. durch das Satzzeichen G(a) abgebildet werden, wenn zwischen dem Zeichen "G" und dem Attribut "Grün", dem Zeichen "a" und der entsprechenden Tatsache "G steht links vor a" und der Tatsache, dass das Attribut dem Ding zugeschrieben wird eine entsprechende Interpretationsregel besteht. Die Kenntnis der Interpretationsregel garantiert, dass man aus dem Satzzeichen dessen deskriptiven Gehalt bzw. dessen Sinn herauslesen kann. Das sagt Satz 4.022 "Der Satz zeigt, wie es sich verhält, wenn er wahr ist. Und er sagt, dass es sich so verhält." Die Abbildtheorie ist unmittelbar nur auf elementare Sätze anwendbar. Die Theorie der Wahrheitsfunktionen macht diese Theorie auch auf logisch komplexe Sätze anwendbar. "...Mein Grundgedanke ist, dass die ‚logischen Konstanten' nicht vertreten. Dass sich die Logik der Tatsachen nicht vertreten lässt." (Satz 4.0312) Der Sinn einer komplexen Aussage ergibt sich somit aus dem wahrheitsfunktional zu ermittelnden - z.B. durch das sog. Wahrheitstafelverfahren - Sinn seiner einfachen Teilaussagen.

Die hier gegebene Skizze der Abbildtheorie des Tractatus lässt sich zwanglos an dem Beweisverfahren von PROLOG exemplifizieren. Wir unterscheiden in PROLOG Anfragen und Datenbanken. Die Datenbanken enthalten Fakten und Regeln. Fakten und Regeln werden auch als Axiome bezeichnet. In einer ersten Annäherung kann man sagen, dass den Anfragen die Wittgensteinschen Satzzeichen und den Axiomen der Datenbanken die Tatsachen entsprechen. Die Einschränkung "in erster Annäherung" ist dadurch motiviert, dass die PROLOG-Anfragen in der Regel die gleiche oder eine ähnliche Gestalt wie die Fakten haben, was den konventionellen Charakter der Gestalt von Satzzeichen verschleiert. Andererseits enthalten die Datenbanken stets sprachlich formulierte Fakten und Regeln, was wiederum den Sachverhalt verschleiert, dass Fakten und Regeln in weitaus naturalistischer Form z.B. als "Realtexte" gegeben sein können. Da - grob gesprochen - die Gestalt der Terme in den Anfragen identisch ist mit der Gestalt ihrer Referenzterme in der Datenbank, kann die Interpretationsregel auf ein "Überdeckungsproblem" reduziert werden, das leicht algorithmisierbar ist.

Von diesen und anderen Defiziten abgesehen, ist das Unifikationsverfahren von PROLOG hervorragend geeignet, der Abbildtheorie eine prozedurale Explikation zu verleihen. Das Abgleichen von Satzzeichen und Tatsachen hinsichtlich Strukturähnlichkeit nach Interpretationsregeln kommt durch das Verfahren der Unifikation von PROLOG-Termen zum Tragen- Dieses Verfahren ist eine algorithmische Prozedur, die zwei Terme auf Isomorphie prüft. Intuitiv sind zwei Terme gleich, wenn sie die gleichen PROLOG-Atomare (Konstanten) sind. Eine Variable kann mit jedem beliebigen Term gleichgesetzt werden. Der Vergleich verschachtelter Terme ist etwas komplizierter: Es müssen die Relationszeichen (auch Funktoren genannt) und die Argumentzahl ermittelt werden; wenn dann auch die Argumente in der Reihenfolge ihres Auftretens jeweils mittels derselben Variablenersetzung unifizierbar sind, sind die beiden Terme gleich. Der Algorithmus der Unifikation ist zu umfangreich, um hier wiedergegeben zu werden. Nach diesem Algorithmus scheitert die Unifikation in folgenden Fällen:

1. Es handelt sich um zwei verschiedene atomare Strukturen.
2. Ein Term ist komplex, der andere atomar.
3. Die Unifikation zweier komplexer Terme scheitert, wenn eines der Kriterien erfüllt ist:
   
   
   • a. Die Funktoren (Relationszeichen) sind verschieden.
   • b. Die Stelligkeit der beiden Funktoren ist verschieden.
   • c. Mindestens ein Argumentpaar von Argumenten gleicher Position im Term lässt sich nicht unifizieren.

Abschließend sei darauf hingewiesen, dass Isomorphie und Unifikation von Strukturen logisch zwar nicht gleichwertig sind, aber zumindest ebenbürtige Explikationen der Metapher der "Überdeckung" strukturgleicher Bilder liefern.