From the ALWS archives: A selection of papers from the International Wittgenstein Symposia in Kirchberg am Wechsel

1. Introduction

What does it mean when we say we can see colours? How do we use them and how do we learn their names? It is not at all clear whether we all experience the same colour when looking at the same red rose. Nevertheless we use the same word and we do understand it when someone else does. We know that red and yellow make orange and that blue and yellow make green, but can we imagine a reddishgreen or a yellowishblue? And why haven’t we got a concept of a white transparent glass?

The problem of colour-incompatibility runs throughout Wittgenstein’s work from Tractatus Logico-Philosophicus (TLP) until On Certainty (OC) and describes a development from ‘logic’ to ‘grammar’ and ‘form of life’. This problem of colour-incompatibility and Wittgenstein’s other remarks on colour have been discussed through the years in several ways (see Literature). In my opinion all these approaches miss a crucial point.

My point is that Wittgenstein is not so much concerned with colours as such, as with our ability to see (that implies both seeing ánd thinking) and our capacity to imagine something. For he links the grammar of colour to the grammar of language through the notion of ‘seeing aspects’: a topic he elaborates extensively in Philosophical Investigations (PI) part II,xi. He relates this notion on the one hand to the colour-octahedron in Philosophical Remarks (PR) and on the other hand to the remarks on colour in Remarks on Colour (RC). Wittgenstein asks questions like: Why haven’t we got a word for a white colour that is fully transparent? We could speak of something white and transparent as being ‘colourless’, but does this term still fall under our notion of colour-concept? It seems that we cannot think of the conceptcombination ‘white water’, because we are not able to describe how something ‘white and transparent’ should look like (cf. RC I-23). What are the limits of our power of imagination?

2. Colour

In my opinion Wittgenstein has deliberately chosen for the colour-octahedron as a 3dimensional model in order to clarify some of the problems concerning the ‘colour grammar’, as he also deliberately has left aside the colour-wheel or Runge’s colour-sphere in his investigations (cf. Gerritsen 1984 and www.colorsystem.com for an extensive overview of coloursystems). Wittgenstein adapts the model of the colour-octahedron from Höfler (Rotthaupt 1996), who follows Hering taking as point of departure the so-called ‘opponent classification’ (in its modern form proposed by Hurvich and Jameson 1957). This classification can be seen as a kind of reversal process according to the formula: red – green, blue – yellow, white – black. Here the basic colour pairs are situated in the model at opposite points. Therefore green is not a mixed colour in this model, but a basic colour. All basic colours are situated on an unambiguous point at the corners of the base; the white-black axis is at right angles to this base.

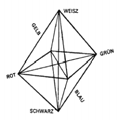Höfler – 1883 (Gerritsen 1984:38)

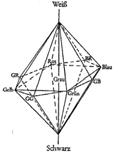Wittgenstein – 1930 (PR-XXI §221)

When we compare Höfler’s octahedron with the one Wittgenstein has drawn, it can be noticed that Wittgenstein is concerned to open up the ‘logical structure’ constructed by the relationships of the colours. This logical structure represents the colour-space in which the rules are laid down: the ‘grammar of colour’. It is important to read Wittgenstein’s colour-octahedron as literally as possible, because only then we can discover why he extended the white-black axis a little upward and downward. In my view he wants to draw with this extension our attention to the fact that this coordinate is situated in a different dimension. This has consequences.

In the first place this so called grey-scale can be seen as an overview of the mixed colours of white and black, but also as a scale of colours between white and black. Secondly in this way can be shown that all saturated colours can be mixed with white, grey tones and black. In that sense the saturated colours (not only the four basic colours) are situated between the opponent pair of white and black. In this respect the oppositions white – yellow – black and red – yellow – green for example have the same structure. The third and most important point Wittgenstein keeps returning on in RC is the fact that we cannot speak of transparent colours in case of this white-black coordinate. According to this model we cannot speak of a transparent white, nor of a transparent grey or black; and that we can observe immediately and ‘in one clear view’ due to the fact that this coordinate is situated in a different dimension. A transparent white would have to lay on a point of one of the lines of the base (cf. RC III-85 and 178).

Another point we can make by comparing the two models is that Wittgenstein has left out the cross inside the base. In doing this he shows us that we can not make a combination with red and green as ‘reddishgreen’ and no combination with yellow and blue as ‘yellowishblue’. On the other hand he divides this square base towards the outside into a regular octagon where he situates the mixed colours ‘somewhere’ between the basic colours. Between these different colours lots of mixed colours can be seen each of them more or less tending towards one of the basic colours; that is greener or more red or even móre red, reddish yellow or bluish green etc. There are no sharp boundaries between the different categories; they are fluid terms we use in daily life in an in principle unlimited variety of cases.

The colour-octahedron is a 3dimensional model capable of showing two dimensions of the colours: the dimension of the four basic colours and their mixed colours on the square base, that can be opaque or transparent in reality, and the dimension at right angles: the white-black axis the one we can only think opaque. In every day life we deal not only with these two dimensions of the colour-octahedron as being an idealized system but also with a depth dimension. This depth dimension shows itself as a 4^th dimension in the reflection, the glittering and shining, and the transparency of the colours (cf. Z 269).

Also in the discovery of the depth dimension Wittgenstein is concerned with the ‘logic’ (that is the grammar) of colour-concepts; he connects this discovery with the ambiguity of colour. Therefore he wonders in RC for example in what ways we differentiate between a transparent representation ‘in a painting’ and the opaque colours ‘on the palette’. And why is it that there can be a transparent green, but no transparent white? Why don’t we have a word for a white colour that is transparent? And when we call it ‘colourless’, does this word still belong to our notion of colour-concept? What is more: when a colour-concept – for example ‘white’ (as a colour-patch) – or ‘transparent’ (as a colour-space) – occurs in just one of the colour geometries: the octahedron or the 4^th dimension – how do we connect these two colour geometries? We could try to neutralize this sort of differences by creating an equal standard, for instance by reducing them to colour-samples as we know from the Munsell system. In that way we are able to compare the two different colour concepts, but only at the expense of the depth dimension. For then we can not differentiate anymore between colour-patch and colour-space (RC I-25).

3. Seeing colours and aspects

We can ‘see something now as luminous, now as grey’ (RC I-38). It is characteristic of Wittgenstein that he links the phenomenon of seeing aspects, investigated in PI II,xi with his inquiries on colour concerning the colour-octahedron in PR and the colour-puzzles in RC. He discovers that seeing aspects is involved in vagueness and in an ambiguity of the notion of ‘seeing’. By taking into account this notion of seeing Wittgenstein is able to extend his grammatical investigations into the broader context of a form of life.

In order to differentiate between the surface dimension and the depth dimension of colours it is not sufficient that we make comparisons the way we do when we call a colour ‘pure red’ the moment we compare that colour with other reds in a same situation. There is no use in comparing between <’colour of gold’ or ‘colour of silver’> and < ‘yellow’ or ‘grey’> (cf. RC III-241). They each belong to a different logical (grammatical) category. We can only get access to the depth dimension of the colours when we are able to make an aspect-change. We see black now as a surface colour now as ‘deep’ or ‘reflecting’. Depending on the context we see the spot now as ‘white’ now as ‘grey’. The change of aspect itself is sharply defined, but the colour-concepts that are involved in that aspect change are ambiguous and context dependent.

Not only in the differentiation of surface and depth dimension do we make use of aspect- change. Also in case of the colour-octahedron Wittgenstein asks us to utilize this ability. According to him the colour-octahedron is a perspicuous representation – übersichtliche Darstellung – of the colour grammar (cf. PR I-II). This concept of ‘übersichtliche Darstellung’ characterizes our form of representation, the way we look at things (PI 122). The model of the colour-octahedron shows us the rules, the connections, we refer to in making decisions concerning the grammar of the colours. Different combinations of the same grammatical rules are possible and some of them can relate to different objects of comparison. Think for example of the fact that red is a colour situated between violet and orange and also between blue and yellow, but is not a mixed colour of violet and orange or blue and yellow. Nevertheless red is the common part of violet and orange. These manners of expression have the advantage that they show us in what ways the colours are defined. However: nothing fixes the rules for ever. The printer or the photographer make use of quite another system than the designer or the decorator.

The purpose of this kind of graphic, 3dimensional and visual model such as the colour-octahedron is to create a change of aspect by illuminating a new application of our words. In his later work Wittgenstein holds that the octahedron, the colour-samples (PI 1) or the standard metre in Paris (PI 50) fulfil a special role in our every day use and get their meaning only in a practice. It is in interaction with the context and with the possibility of making analogies with situations in concrete practices that these models (also) make meaning possible. The colour-octahedron for instance is an übersichtliche Darstellung for a certain part of the colour grammar, but falls short in representing the depth dimension of the colours. It is not so much suited for the arrangement but for an arrangement (cf. PI 132). We only can describe the glittering, reflection or transparency of a colour within the broader context in which they appear. This context brings them to life so to speak.

Wittgenstein repeatedly takes the glittering and the reflection as a subject of inquiry in his colour-puzzles in order to illuminate on the one hand the similarities and differences between those two concepts and on the other hand to show the connection with transparency. The differences between ‘black’ and ‘dark’ and between ‘cloudiness’ (opaque) and ‘deep’ (transparent). The concept ‘white’ related to transparency, glittering, the relation white – grey and ‘white’ related to ‘substance colour’. The investigation into ‘white’ and ‘grey’ is connected with surroundings, like the different ways of illumination that make a colour-spot on one time appear as white, the other time as grey. The incidence of light seems to make a colour look differently; but does not make it different.

Our conceptual domain is fluid and flexible; Wittgenstein suggests that we could even invent a natural history. A totally different world would imply totally different concepts. He draws our attention to experiments that have the form of ‘trying to imagine something’ by means of the colour-puzzles (PR and RC) and the perception-puzzles (PI II,xi). Seeing aspects asks for the power and the ability of imagination. The answer to the question why we cannot think of a ‘fully transparent white’ is as simple as it is compelling: the expression ‘transparent white’ does not fit into our form of life, our picture of the world. We just have no use for it. When we have to name it, we call it ‘colourless’, but then it is not at all clear whether this expression still falls under our concept of colour (cf. PI 115 and RC III-210, 217). It is our picture of the world that is constitutive for our convictions and our language. It is the inherited background to which we decide between true and false (OC 94).

4. Conclusion

Apparently we have words for things that do not exist in reality: words like ‘grey-glowing’ or ‘illuminating-grey’ have no representation in reality. In addition we cannot find any words for things that do exist in reality: every painter knows that making a transparent white is no problem at all. A handful of flour thrown in a bucket full of water and there we have a beautiful transparent white. Yet we cannot think a transparent white! From this angle we can say that the investigations concerning the colours is an investigation that has the limits of our thinking, of our imagination in its centre. The scope of our ability to discover new links by means of seeing aspects implies the scope of our imagination. This scope is related to our form of life. In this respect the investigations of Wittgenstein direct us to an anthropological interpretation.