From the ALWS archives: A selection of papers from the International Wittgenstein Symposia in Kirchberg am Wechsel

Einleitung

Auf der 2. Tagung für Erkenntnislehre der exakten Wissenschaft in Königsberg 1930 sollten die unterschiedlichen Ansätze in den Grundlagen der Mathematik dargestellt werden: Carnap referierte über den Logizismus, Heyting über den Intuitionismus, Neumann über den Formalismus (vgl. Hahn et al. 1931). Interessanterweise wurde neben diesen Ansätzen noch ein vierter Ansatz dargestellt: Der Standpunkt Wittgensteins, über den Friedrich Waismann vortrug. Waismann tat dies mit der Unterstützung Wittgensteins, was zeigt, dass Wittgenstein keineswegs den Anspruch ablehnte, eine alternative Position in den Grundlagenfragen der Mathematik einzunehmen. Das Schicksal, das Waismanns Versuch erfuhr, Wittgensteins Standpunkt zu kommunizieren, ist symptomatisch: Waismann gelang es im Unterschied zu den anderen Referenten nicht, seinen Vortrag in eine publizierfähige Form zu bringen. Ein erhaltenes Skript (vgl. Waismann 1982) ist unvollständig und beschäftigt sich vornehmlich mit Wittgensteins Kritik am Logizismus; eine eigenständige Motivation für einen alternativen Standpunkt entfaltet Waismann nicht. In der anschliessenden Diskussion der Referate wurde Wittgensteins Standpunkt übergangen, da er noch nicht in einer „spruchreifen Form“ (Hahn et al. 1931, S. 141) vorlag. Die Rezeption von Wittgensteins Standpunkt scheiterte auch bei gutwilligen und mit der Materie vertrauten Forschern, da es nicht gelang, diesen als eine konstruktive Alternative zu identifizieren und verständlich zu machen.

Im Unterschied zu der Wahrnehmung der Zeitgenossen Wittgensteins, wird in der Sekundärliteratur Wittgensteins Position meist so verstanden, dass er keine echte Alternative zu bestehenden Ansätzen in der Grundlegung der Mathematik bietet: Baker und Hacker meinen, Wittgensteins Philosophie der Mathematik beträfe ausschliesslich die Kritik der Voraussetzungen grundlagentheoretischer Ansätze und impliziere keine konstruktive Alternative (z.B. Baker & Hacker 1985, S. 345); andere prominente Interpreten verstehen Wittgensteins Position hingegen als eine Form des Konstruktivismus (z.B. Frascolla 1994, Marion 1998, Mancosu & Marion 2002).

Demgegenüber soll im Folgenden der Erwartungshaltung von Wittgensteins Zeitgenossen um 1930 Recht gegeben werden: Wittgensteins Standpunkt lässt sich als eine Alternative zu Grundlegungsversuchen in der Logik und Mathematik verstehen – allerdings blieb sein Ansatz Programm. Wittgenstein arbeitete sein Programm nicht aus, sondern beschäftige sich unter Voraussetzung der Durchführbarkeit seines Programmes ab Ende der 20er Jahre vornehmlich mit der Kritik alternativer Positionen und der Frage der Interpretation mathematischer Theoreme und Beweise.

Der Schlüssel zum Verständnis der Position Wittgensteins als einem alternativen grund-lagentheoretischen Ansatz liegt in seinem Verständnis logischer Beweise, das er in seiner Frühphilosophie in kritischer Auseinandersetzung mit Freges und Russells axiomatischem Beweisverständnis entwickelt. Dies soll im Folgenden skizziert werden.

1. Alte vs. Neue Logik

Wittgenstein unterscheidet bereits in den Notes on Logic (NL) und den Moore Notes (MN) eine „alte“ und eine „neue Logik”. Er markiert hiermit keineswegs die einschneidenden Entwicklungen in der Logik seit Peano, Frege und Russell; vielmehr charakterisiert er durch die „alte Logik“ die auf einem axiomatischen Beweisverständnis beruhenden Kalküle Freges und Russells, und grenzt von diesen sein eigenes Verständnis der Logik ab. In den MN, S. 109[5] beschreibt Wittgenstein das „Vorgehen der alten Logik“:

This is the actual procedure of [the] old Logic: it gives so-called primitive propositions; so-called rules of deduction; and then says that what you get by applying the rules to the propositions is a logical proposition that you have proved.

Was Wittgenstein hier beschreibt, ist das gewöhnliche Verständnis logischer Beweise im Sinne von Ableitungen innerhalb eines Axiomensystems: Dass eine Formel allgemeingültig ist, wird bewiesen, indem sie aus Axiomen mittels Schlussregeln abgeleitet wird. Wittgenstein leugnet nicht, dass durch dieses Verfahren allgemeingültige Formeln (Tautologien) identifiziert werden können, aber er stellt in Frage, dass auf diese Weise ihre Allgemeingültigkeit (d.i. logische Wahrheit) bewiesen werden kann. Direkt im Anschluss an das angegebene Zitat, fährt er fort (MN, S. 109[5]):

The truth is, it tells you something about the kind of proposition you have got, viz that it can be derived from the first symbols by these rules of combination (= is a tautology).[…] The so-called proof of a logical proposition does not prove its truth […].

Alles, was bewiesen wird, ist die Ableitbarkeit der Formeln aus den Axiomen. Nur unter der Voraussetzung der logischen Wahrheit der Axiome kann hieraus auf die logische Wahrheit der Formeln geschlossen werden: Diese Voraussetzung ist aber nicht mehr innerhalb des Axiomensystems beweisbar, da es innerhalb dieses Systems kein unabhängiges Kriterium gibt, durch das Axiome von anderen, nicht logisch wahren Formeln unterschieden werden können – die Axiome lassen sich nur durch willkürliche Festlegung als logisch wahre Formeln identifizieren. Das Problem axiomatischer Beweise besteht darin, kein syntaktisches Kriterium für logische Eigenschaften beliebiger Formeln eines Formelsystems anzugeben. Nach dem gewöhnlichen Verständnis logischer Beweise im Sinne von Ableitungen bleibt man auf Beweise der logischen Wahrheit der Axiome angewiesen, die nicht mehr innerhalb der formalen Logik geführt werden können. Hierdurch stellt sich die Frage nach einer ausserlogischen oder metalogischen Grundlegung der Axiome. Eine derartige Grundlegung überschreitet nach Wittgenstein aber notgedrungen den Rahmen zulässiger Beweisgründe in der Logik: Ziel einer derartigen Grundlegung ist letztlich, die logische Wahrheit oder Widerspruchsfreiheit durch die subjektive Evidenz inhaltlicher Beweisführungen zu sichern – die Bezugnahme auf eine subjektive Evidenz ist jedoch kein zulässiges Kriterium der logischen Wahrheit oder der Widerspruchsfreiheit der Axiome (Philosophische Grammatik (PG), S.297) :

Die Logik und die Mathematik ruht nicht auf Axiomen; […]. Hierin liegt der Fehler, dasEinleuchten, die Evidenz, der Grundgesetze als Kriterium der Richtigkeit in der Logik zu betrachten.

Zielsetzung von Wittgensteins „neuer Logik“ ist es, axiomatische Beweisverfahren durch Beweisverfahren zu ersetzen, die nicht auf eine Grundlegung von Axiomen angewiesen sind. In Bemerkung 6.1265f. des Tractatus (TLP) schreibt er:

Immer kann man die Logik so auffassen, dass jeder Satz sein eigener Beweis ist.

Alle Sätze der Logik sind gleichberechtigt, es gibt unter ihnen nicht wesentlich Grundgesetze und abgeleitete Sätze.

Jede Tautologie zeigt selbst, dass sie eine Tautologie ist.

Diese kryptische und zirkulär klingende Formulierung einer nicht-axiomatischen Beweisführung wird erst verständlich, wenn man sich das von Wittgenstein entwickelte logische Beweisverfahren vor Augen führt. Dies ist nicht etwa, wie oft angenommen wird, die gängige Methode der Wahrheitswerttabellen, sondern die Transformation logischer Formeln in die ab-Notation: Dieses Verfahren entwickelte Wittgenstein 1913 – es stellt für ihn das Beweisverfahren der „neuen Logik“ dar. Wittgenstein beschreibt dieses Verfahren an keiner Stelle eingehend. Er gibt allerdings einige Beispiele, die deutlich machen, wie prädikatenlogische Formeln in die ab-Notation zu transformieren sind, und einige Bemerkungen belegen, welchen Stellenwert er der ab-Notation zuschrieb.

In seinem Brief vom November und Dezember 1913 an Russell (Cambridge Letters (CL), Brief 32) gibt Wittgenstein als ab-Zeichen der aussagenlogischen Formel p ↔ p an:

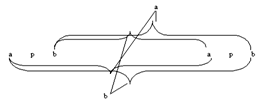
Allgemein wird ein ab-Zeichen einer aussagenlogischen Formel gebildet, indem man alle in der Formel vorkommenden Satzbuchstaben – seien sie identisch oder unterschiedlich – links mit einem a- und rechts mit b-Pol versieht, und die Wahrheitsfunktionen zwischen den Satzbuchstaben durch ab-Funktionen widergibt. Ab-Funktionen sind Funktionen, die den a- bzw. b-Polen bzw. Polpaaren wiederum a- bzw. b-Pole zuordnen. Es gibt eine ab-Funktion, die einem Pol wiederum einen Pol zuordnet: Dem a-Pol den b-Pol und dem b-Pol den a-Pol – durch diese wird die Negation abgebildet. Es gibt 14 ab-Funktionen, die den 4 Polpaaren aa, ab, ba, bb wiederum a- bzw. b-Pole zuordnen. Diese 14 Funktionen bilden dyadische Wahrheitsfunktionen ab. Da keine ab-Funktion allen 4 Polpaaren nur einen Pol zuordnet, und da stets Zuordnungen zu demselben Pol zusammengefasst werden, erhält man durch die erneute Verknüpfung der Pole (dargestellt durch Klammern) stets die vier möglichen Polpaare aa, ab, ba, bb als Argumente.

Als Regel für die Entscheidung darüber, ob eine beliebige aussagenlogische Formel eine logisch wahre oder logische falsche Formel ist, nennt Wittgenstein Russell gegenüber die folgende (CL, Brief 30):

[…] write the prop[osition] down in the ab-Notation, trace all Connections (of Poles) from the outside to the inside Poles: Then if the b-Pole is connected to such groups of inside Poles ONLY as contain opposite poles of ONE prop[osition], the whole prop[osition] is a true, logical prop[osition]. If on the other hand this is the case with the a-Pole the prop[osition] is false and logical.

Demnach ist anhand des ab-Zeichens der Formel p ↔ p zu entscheiden, dass die Formel logisch wahr ist, da der äussere b-Pol des ab-Zeichens nur entgegengesetzten innersten Polen desselben Satzbuchstabens p zugeordnet ist.

Wittgenstein betont Russell gegenüber, dass es nicht auf die besonderen Regeln der ab-Notation ankommt, sondern darauf, dass es möglich ist, ein allgemeines Transformationsverfahren zu definieren, durch das für eine beliebige aussagenlogische Formel entschieden werden kann, ob diese logisch wahr oder logisch falsch ist (CL, Brief 30):

That means that there is one Method of proving or disproving all logical prop[osition]s and this is: writing them down in the ab-Notation and looking at the connections and applying the above rule.

Wittgenstein interpretiert sein Transformationsverfahren aussagenlogischer Formeln in ab-Zeichen als Entscheidungsverfahren: Im Unterschied zu Ableitungen handelt es sich nicht um ein Transformationsverfahren innerhalb ein und derselben Formelsprache, sondern um die Transformation von Formeln einer Formelsprache (im beschriebenen Fall der Aussagenlogik), anhand von deren Merkmalen es nicht möglich ist, logische Eigenschaften der Formeln zu identifizieren, in Formeln einer anderen Formelsprache (im beschriebenen Fall in ab-Zeichen), anhand von deren äusseren Merkmalen es möglich ist, die logischen Eigenschaften der Formeln zu identifizieren. Ein derartiges Beweisverfahren ist weder auf Axiome angewiesen, noch bedarf es der Bezugnahme auf Interpretationen der Formeln. Es liefert ein allgemeines syntaktisches Identifikationskriterium logisch wahrer und logisch falscher Sätze, das ausschliesslich auf objektive Beweisgründe – Merkmale von Formeln einer beweisenden Notation – rekurriert.

Wenn Wittgenstein schreibt, dass jeder logische Satz sein „eigener Beweis“ ist und dass jede Tautologie „selbst zeigt, dass sie eine Tautologie ist“, dann setzt er hierbei die Transformation logischer Formeln in eine zum Zwecke der Identifikation logischer Eigenschaften definierten Notation voraus (vgl. TLP 6.122).

Wittgensteins Motiv, ein gegenüber dem klassischen, axiomatischen Beweisverständnis alternatives Beweisverfahren zu entwickeln, ist ein grund-lagentheoretisches: Er will jegliche ausserlogischen und metalogischen Fundierungsversuche durch eine Definition von Transformationsverfahren überflüssig machen, durch die für beliebige Formeln eines Formelsystems anhand syntaktischer Merkmale entschieden werden kann, ob sie bestimmte logische Eigenschaften haben oder nicht. Nach diesem Ansatz ist die Zielsetzung grundlagentheoretischer Ansätze verfehlt, das Fundament von Beweisverfahren (die Axiome) zu rechtfertigen, und stattdessen die grundlagentheoretische Aufgabe darin zu sehen, mechanisierbare Transformationsverfahren von Formelsystemen zu definieren, die auf keinerlei inhaltliche Beweisführungen angewiesen bleiben.

2. Prädikatenlogik

Wittgensteins Ansatz steht und fällt nach diesem Verständnis damit, ob sich das Programm der Definition von Entscheidungsverfahren im Sinne von Transformationsverfahren über die Aussagenlogik hinaus realisieren lässt. Wiederholt erwähnt Wittgenstein gegenüber Russell in seinen Briefen, dass er nicht daran zweifelt, dass die ab-Notation auch ein Entscheidungsverfahren für die Prädikatenlogik liefert. Es gibt jedoch nur eine einzige Bemerkung, in der er die ab-Notation einer prädikatenlogischen Formel angibt (NL, S. 11[3]):

The application of the ab notation to apparent variable propositions becomes clear if we consider that, for instance, the proposition “for all x, φx” is to be true when φx ist true for all x’s and false when φx is false for some x’s. We see that some and all occur simultaneously in the proper apparent variable notation.

The notation is:

for (x)φx: a-(x)-aφxb-(∃x)-b and

for (∃x)φx: a-(∃x)-aφxb-(x)-b

Old definitions now become tautologous.

Wittgenstein hält auch für die Prädikatenlogik an einer Polschreibweise fest. Im Unterschied zur Aussagenlogik enthalten die Pole auch Quantoren. Die Entscheidungsregeln für logische Wahrheit und logische Falschheit quantorenlogischer Formeln sind dementsprechend für komplexere Pole zu definieren. Wittgenstein setzt eine derartige Entscheidungsregel voraus, wenn er anschliessend konstatiert, dass „alte Definitionen“ durch die ab-Notation als Tautologien identifiziert werden können. Er bezieht sich hierbei auf Quantorendefinitionen, die Russell und Whitehead in den Principia Mathematica (PM) einführen. Proposition 9.01 der Principia lautet (PM, S. 130):

*9.01 ~(x).φx . = . (∃x).~φx Df

Die ab-Notation für ~(x).φx ist: b-a-(x)-aφxb-(∃x)-b-a

Die ab-Notation für (∃x).~φx ist: a-(∃x)-baφxba-(x)-b

Hier ist jeweils der äusserste a-Pol über den Existenzquantor dem inneren b-Pol von φx, und der äusserste b-Pol über den Allquantor dem inneren a-Pol von φx zugeordnet: Die Äquivalenz der Formeln lässt sich durch Bezugnahme auf den äussersten Pol, dem jeweiligen Quantor, der zwischen den äusseren und den inneren Polen steht, sowie dem inneren Pol, d.i. dem äussersten Pol der Polreihe, die zwischen Aussagefunktion und Quantor steht, identifizieren. Der entscheidende Punkt ist hier wiederum der, dass durch die ab-Notation für quantorenlogische Formeln Grundgesetze (vgl. für *9.1 und *9.11 der PM CL, Brief 30) und Definitionen, die innerhalb eines axiomatischen Kalküls ohne Beweis eingeführt werden, beweisbar sind.

Es stellt sich die Frage, ob eine allgemeine Transformationsregel prädikatenlogischer Formeln in die ab-Notation und eine allgemeine Entscheidungsregel für logische Wahrheit und logische Falschheit in Bezug auf die ab-Zeichen definiert werden kann. Dass Wittgenstein derartige Regeln im Tractatus nicht angibt, ist kein Beweis dafür, dass ihm Zweifel an der ab-Notation bzw. allgemein an der Durchführbarkeit seines Programmes kamen – im Gegenteil seine Ausführungen zu logischen Beweisen im Tractatus (TLP 6.1ff.) setzen die Durchführbarkeit seines Programmes im Rahmen der Quantorenlogik voraus. Es wäre unmöglich, etwaige Regeln im Rahmen der Quantorenlogik in ähnlich knapper Weise wie für die Aussagenlogik anzugeben. Die Form des Tractatus würde gesprengt, wenn Wittgenstein seine ab-Notation hier ausgeführt hätte. Schon in der publizierten Form fällt die erst im Gefangenenlager von ihm hinzugefügte Bemerkung 6.1203, die eine der ab-Notation analoge Klammernotation für aussagenlogische Formeln einführt, auf Grund ihrer Länge aus dem Rahmen.

3. Identität

Im Unterschied zur Prädikatenlogik ohne Identität, für die Wittgenstein eine Definition der ab-Notation offensichtlich für unproblematisch hielt, spricht er in den Briefen an Russell wiederholt von dem Problem, die ab-Notation auch für die Identität zu definieren (CL, Brief 30 und 32, vgl. auch 24 auch 34). Aber auch hier betont er, dass er nicht daran zweifelt, dass sich eine Notation finden lässt, durch die auch die logische Wahrheit und logische Falschheit von Formeln der erweiterten Prädikatenlogik entschieden werden kann. Das Problem der Identität löst Wittgenstein im Tractatus aber schliesslich nicht auf die Weise, dass er ein Transformationsverfahren für beliebige Formeln der klassischen erweiterten Quantorenlogik voraussetzt, sondern durch die Voraussetzung einer exklusiven Deutung der Quantoren, durch die die Verwendung des Identitätszeichens für eine grosse Klasse von Formeln überflüssig wird: z.B. kann die Formel ∃xFx & ∀x,y (Fx & Fy Π x = y) unter Voraussetzung einer exklusiven Formalisierung durch ∃x Fx & ¬∃x,y (Fx & Fy) wiedergegeben werden (vgl. TLP 5.5321). Andere Formeln, die nicht unter Voraussetzung einer exklusiven Deutung der Quantoren wiedergegeben werden können – z.B. a = a oder ∀x x = x – verwirft er unter der Annahme, dass diese keine sinnvolle Interpretation besitzen (TLP 5.534). Unter Voraussetzung einer exklusiven Deutung eliminiert Wittgenstein das Identitätszeichen aus inklusiv gedeuteten prädikatenlogischen Formeln: Eines speziellen Transformationsverfahrens für Formeln, die das Identitätszeichen enthalten, bedarf es unter dieser Voraussetzung nicht mehr – das Problem ist reduziert auf das der Definition eines Transformations- bzw. Entscheidungsverfahrens für exklusiv gedeutete prädikatenlogische Formeln. Auch Wittgensteins exklusive Deutung der Quantoren ist im Rahmen des Programms zu verstehen, nicht-axiomatische Beweisverfahren zu definieren.

4. Ausblick: Metamathematik und Grundlagen der Mathematik

Wittgensteins Standpunkt steht im Gegensatz zu den Ergebnissen der Metamathematik und den unterschiedlichen Ansätzen in der Grundlegung der Mathematik. Es gilt als bewiesen, dass die Prädikatenlogik unentscheidbar ist (Church1936). Die Ansätze zur Grundlegung der Mathematik gehen von einem axiomatischen Beweisverständnis aus, und beantworten die Frage nach der Grundlegung von Axiomen entweder durch Reduktion auf andere Axiome, die nicht weiter begründet werden (Logizismus), oder durch eine ausserlogische Grundlage (Intutionismus bzw. Konstruktivismus) oder durch eine metamathematische Begründung (Formalismus). Wittgensteins Standpunkt würde demgegenüber in Anwendung auf Grundlagenfragen der Mathematik fordern, dass auch für arithmetische Formelsysteme Entscheidungsverfahren im Sinne von Transformationsverfahren zu definieren sind – Wittgensteins Bemerkungen zu Beweisen mathematischer Gleichungen im Tractatus (vgl. 6.2ff.) setzen die Realisierbarkeit dieses Programmes voraus und enthalten Andeutungen (vgl. 6.241), wie es unter Voraussetzung seiner Zahldefinition (vgl. 6.02ff.) in dem einfachen Fall von Zahlgleichungen, die nur das Additions- und Multiplikationszeichen enthalten, durchzuführen ist. Die Annahme der Durchführbarkeit des Programmes für beliebige arithmetische Systeme, die nicht nur Ziffern und Operationssymbole, sondern auch freie Variablen enthalten, widerspricht den arithmetischen Unentscheidbarkeitsbeweisen (vgl. z.B. Hilbert 1970, S. 433).

Es liegt nahe, Wittgensteins Ansatz unter Voraussetzung der metamathematischen Beweise als undurchführbar abzulehnen. Die einzige Alternative, die es unter Voraussetzung von Wittgensteins Standpunkt hierzu gibt, ist eine Kritik der Metamathematik. Wittgenstein ging diesen Weg, ohne dabei die Ausarbeitung von Entscheidungsverfahren weiter zu verfolgen.

Der direktere Weg, dem Standpunkt Wittgensteins gegenüber den Resultaten der Metamathematik Recht zu geben, bestände darin, durch Definition eines Entscheidungsverfahrens für die Prädikatenlogik im Sinne Wittgensteins Churchs Unentscheidbarkeitsbeweis der Prädikatenlogik sowie den diesem Unentscheidbarkeitsbeweis zugrunde liegenden Unentscheidbarkeitsbeweis der Arithmetik direkt zu widerlegen. Nur unter dieser Voraussetzung kehrte sich die Beweislast um: Nicht mehr die Durchführbarkeit von Wittgensteins Programm, sondern die Beweiskraft metamathematischer Beweise stünde in Frage.