From the ALWS archives: A selection of papers from the International Wittgenstein Symposia in Kirchberg am Wechsel

1. Introduction

The focus of this paper is on the possible educational uses of an ancient Chinese artifact. The intercultural perspective (Abdallah-Pretceille 1999) is important from the educational viewpoint: it is based upon the identification and the celebration of the diversity that history of mathematics itself can show us (Grugnetti and Rogers 2000), and upon the interaction which makes possible the educational use of the experiments considered. A recent study (Bagni 2006) considers an educational experiment based on the use of an ancient Chinese artifact.

The traditional Chinese representation of numbers by means of counting rods on a board can be referred to the fingers of a hand:

The counting rods are arranged in columns placed side by side, with the right-most column representing the units, the next column representing the tens, and so on. Before the 7th – 8th cent. AD, there were no known written Chinese symbols interpreted as zero (Martzloff 1997), so in order to avoid misunderstandings Chinese mathematicians used two different dispositions: the aforementioned Tsung disposition for units, thousands and so on, and the Heng for tens, hundreds and so on.

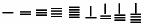
2. Theoretical Framework

According to Vygotsky, the function of semiotic mediation can be connected to technical and psychological tools (Vygotskij 1978). Wartofsky identifies technical tools as primary artifacts; secondary artifacts are used to preserve and to transmit the acquired skills or “modes of action” (Wartofsky 1985). So countingrods can be considered as primary artifacts; prescriptions and representative rules (expressed in original books and commentaries) are secondary artifacts. A mathematical theory is a tertiary artifact which organizes the secondary artifacts and hence the models constructed in order to represent the modes of action by which primary artifacts are used (Bartolini Bussi 2002).

We must consider the distinction between artifact and tool (Rabardel 1995), i.e., the artifact associated to a personal or social schema of action: if we refer to an object as artifact, in order to be able to consider it as a tool, we need a constructive mediated activity on the part of the subject (Radford 2002). Thus the artifact in question must be framed into a wider social and cultural context. When a pupil uses a primary artefact with reference to a secondary artifact, he or she follows the rules and thus uses the primary artifact in a rational way. There is an important socio-cultural element in this, if one takes into account that rule-following must be framed in an essentially collective practice (for instance, with reference to Wittgenstein’s use of the considered expression, see: Kripke 1984 and Wright 1980). Let us note that, according to Habermas, the rationality has three different roots, strictly related the one to the others: the predicative structure of knowledge at institutional level, the teleological structure of the action and the communicative structure of the discourse (Habermas 1999); of course these roots are influenced by different cultural traditions.

According to Bruner’s constructivist approach, we, too, create our own realities through interaction with the social world and with symbols (Bruner 1987): learning itself must be considered within a cultural context, which involves the shared symbols of a community, its tools, its traditions (Bruner 1996; in Bruner 1991, the author asserts that culturally shaped notions, stories, and narratives organize our experience and expectations). The doctrine of meaning as use (Wittgenstein 1953, § 43) implies that the key concept is that of context embeddedness, where the term refers to the institutional and cultural context (Godino and Batanero 1997). So an aspect to be considered is the context in which we are going to propose an activity with counting rods: as a matter of fact, pupils were not asked to approach an explicit mathematical (algebraic) activity. As we shall see, the method they used can be approached as a new game, which is not included in the usual cultural system, not as a traditional mathematical task.

3. Methodology

In this paper we make reference to the chapter 8 (Fangcheng) of the Jiuzhang Suanshu (Nine Chapters on the Mathematical Art, 1st cent. BC), an anonymous handbook containing 246 problems (Cullen 2002). In order to solve a system of linear equations, ancient Chinese mathematicians placed coefficients and numbers on the counting board; their arrangement can be changed according to the following rules: the expression biancheng (“multiplication throughout”, Martzloff 1997, p. 253; Needham 1959) is an instruction to multiply all the terms of a row by a given number; the expression zhichu (“direct reduction”) carries out a series of term-by-term subtractions of a row from another row.

We are going to summarize an experiment with a group of 11-year-old pupils. The experience took place in a 6th grade classroom (in Treviso, Italy). The experimental excerpts (Bagni 2006) allowed us to highlight some elements that are relevant to our discussion.

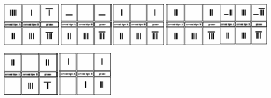
Let us consider the system (in our modern notation):

    5x + 3y = 19

    3x + 2y = 12

and let us see the rods arrangements proposed by some pupils in order to obtain the solution (we report the original counting board used; the translation of the labels is: “type A” and “type B bundles”, “cereals”):

Let us consider now the second system (in our notation):

    4x + y = 6

    2x + 3y = 8

and the solution proposed by the same group of pupils:

4. Discussion

In the experiment in question, pupils approached an algebraic procedure without using the typical algebraic signs. They effectively solved a couple of simultaneous linear equations by using counting rods, thus with reference to the secondary artifact expressed in chapter 8 of the Jiuzhang Suanshu.

According to Bruner, developmental growth considers the enactive, iconic and symbolic modes, and requires ability to translate between them (Bruner 1987): the experiment in question provides us with interesting examples of translation. An effective translation from the enactive to iconic mode (the frequent use of deictic expressions and of gestures is remembered in: Bagni 2006) and, in addition, a first approach to the symbolic mode can be seen in the pupils’ behaviour.

Pupils gave preference to the rule that is based more directly upon the concrete presence of counting-rods on the counting board. Indeed, when they apply rule zhichu (“direct reduction”), which allows term-by-term subtractions of two rows, they consider two quantities that they can see and touch; whereas when they apply rule biancheng (“multiplication throughout”), which allows the multiplication of all the terms of a row by a number k, this number k cannot be referred to the concrete presence of counting-rods. So, according to the empirical data, we can state that using (original) primary artifacts with reference to (original) secondary artifacts can be relevant to the introduction of some methods; more generally, the crucial point is that the considered method is based upon the “positional” character of ancient Chinese algebra, according to which a particular place in the board must be always occupied by a particular kind of number (e.g. a particular coefficient). This “positional” character cannot be pointed out in our basic algebraic European tradition.

What is the transparency (Meira 1998) of the artifact in question? Pupils used a representation including signs, spatial relations and embodied rules with reference to a context having some typical features of a game, more precisely of a new game (concerning multicultural games, a lot of references can be quoted; for instance: Barbarash 1999; Kirchner 2000; Braman 2002; several mathematical games are examined in: Zaslavsky 1998). So an important path to follow can be related to the role of the game: this concrete context may allow the effective construction of meanings that can be referred to abstract algebraic representation.

It is worth noting that the secondary artifact introduced is not strictly necessary in order to allow a physical action with the primary artifact: from this point of view, the introduced rules can be considered conventional, arbitrary (the original secondary artifact can be simplified: for instance, the use of both Tsung and Heng dispositions is not strictly necessary: counting rods can be arranged in very many ways; of course the intercultural aspect leads us to refer to the original dispositions). So pupils referred to a particular algebraic “language” that “did not emerge from some kind of ratiocination” (Wittgenstein 1969, § 475): in fact, the origin of a language game is a reaction. Following Wittgenstein, we can remember that language is not just a code, whose power can be referred to its syntax; its creative power lies in how language itself is embedded in the rest of pupils’ activities, and, in this particular case, in a game. The game has a well-defined meaning in the pupil’s mind, being a new game to be explored and played; we are dealing with a game making reference to a very different cultural tradition: and this meaning is clearly useful in order to give sense to the algebraic procedure considered.

Of course, it is important to investigate the conceptualization of the experience, in order to avoid the meaning of the procedure introduced being considered only in the sense of know how and not in the sense of know that (Wittgenstein 1956, I § 99 and II § 46): further research will be devoted to the study of the educational possibilities connected to activities similar to the one considered. However, in our opinion, the main point cannot be summarised in the possibility of a complete derivation of an argumentation, or a mathematical proof (Balacheff 1987): as a matter of fact, pupils will develop the connection with the predicative structure of knowledge at an institutional level in the process of teaching and learning.

Finally, we should point out that the experiment described can be regarded as an intercultural opportunity for proposing a mathematical content with reference to the context in which it was actually developed. All over the world, in all historical periods, people have developed mathematical ideas to meet their needs and interests. This perspective can thus enrich the learning of all students: they learn that mathematics was created by real people attempting to solve real problems and they are asked to extend their problem solving skills to issues within their communities. It should be remembered that Rorty underlines the importance of the relativity of descriptive vocabularies to periods and traditions (Rorty 1979). Nevertheless, pupils of different interests and diverse achievement levels will take pride in the contributions of their own people and learn to appreciate the accomplishments of others. Education is an instrument for promoting understanding and dialogue between cultures: really overcoming prejudice and obstructing the emergence of intolerance are primary educational tasks.