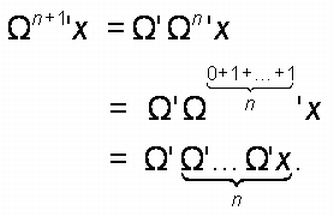From the ALWS archives: A selection of papers from the International Wittgenstein Symposia in Kirchberg am Wechsel

• Home
• About
• Login
• Search
• Current
• Archives

Table of contents

• Literature

The Stanford Encyclopedia of Philosophy says that Wittgenstein is a logical atomist in the Tractatus. My position is that logical atomism is inessential within Wittgenstein's philosophy. For him a pellucid logical analysis does not require that elementary arithmetic actually be part of logic. The logical atomist interpretation takes general propositions about elementary arithmetic to depend on logic in the sense of a truth-functional analysis. I argue that in the Tractatus the truth-functional analysis and the concept of natural number depend on the operation.

The position that Ludwig Wittgenstein is a logical atomist when he writes the Tractatus Logico-Philosophicus has become mainstream in the new millennium, even though it was originally a speculative revision of the traditional interpretation that Wittgenstein is a logicist in the Tractatus. The author of the Stanford Encyclopedia article, Ian Proops, acknowledges his claim is controversial.

One reason this position remains philosophically controversial even after wide acceptance is that Wittgenstein himself never claimed to be a logical atomist. Logical atomism normally has been thought to be a branch of philosophy developed by Bertrand Russell in the years after the publication of the first volume of the Principia Mathematica. Today I shall argue that, from the perspective of the philosophy of mathematics, Wittgenstein could have been a logical atomist only in a derivative sense. I shall sketch what I take to be the central view of logical analysis in the Tractatus, and end with the proposition I find evident in that sketch, that logic is an ideal in the Tractatus.

*

There are five core tenets of logical atomism, but only one main idea for my purposes. This main idea is to express a generality as a logical product.¹ For example, to express 'All my friends love the ocean' it suffices to express a conjunction of elementary propositions each of which manifests one of my friends liking the ocean. That is, I can write:

• Dennis loves the ocean AND Donna loves the ocean AND Genia loves the ocean AND Greg loves the ocean AND Nir loves the ocean AND SO ON.

The conjunction 'AND' is what we would call a "logical constant"; however, in the Tractatus, strictly speaking, there are no logical constants (5.4).²

Let's look at this point more closely. Wittgenstein reduces the general form of any proposition to the truth-functional calculus specified and determined by the notion of the iteration of an operation. My immediate purpose is to explain that determination. In the Tractatus, every non-elementary proposition results from successive applications of the N operator to some elementary propositions, as follows:

• [a, N, N’a].

This is the general form of the proposition, a mnemonic device for which is Anna: the A is an elementary proposition (or a collection of elementary propositions), the n is a truth-functional operation, and the na is the result of applying n to a. Anna is a variable going proxy for any truth-functional proposition. It gives the variable form of the logical product about my friends loving the ocean, where A is a series of elementary propositions, one for each friend, and n is conjunction.

Anna, a recursive variable providing the general form of the truth-function, appears in the Tractatus as

• [̅p, ̅ξ, N(̅ξ)] (6).

I apologize for putting Anna so formally, but I want you to see what I take Wittgenstein to mean when he writes that an "operation shows itself in a variable" (5.24) by giving the difference and showing how to proceed. Say, e.g., the variable is a, x gives the difference, and O'x shows how to proceed. Then the propositional variable

• [a, x, O'x] (5.2522)

is the formal component of the general form of the Omega operation Ω'(̅η) (6.01). Set ̅η, the variable basis of the Omega operation, to be some series of propositions ̅p, then

• [̅p, ̅ξ, N(̅ξ)] = [̅ξ, N(̅ξ)]'(̅p).

This, Wittgenstein writes, "is the most general form of transition from one proposition to another" (6.01). In sum, the interpretation of Wittgenstein as a logical atomist does not violate the interpretative requirement imposed by Brian McGuinness that there be no logical constants only if Anna is provided for by the Omega operation.

The general case is supposed to involve a complete description. A complete description of everything I have written in my pocket notebook includes each of the entries plus the proposition that there are no other entries in my pocket notebook. I've been trying to convince you that the generality of Anna derives from the Omega operation; having exposed the operation as the generator for any logical connection between propositions, I shall take up the question of the logical analysis of generality in mathematics. Previous commentators have all focused on Anna, but my focus is on what is essential to the general form, which, I shall now argue, is the iteration of an operation, the 'AND SO ON' in the logical product about the ocean. In the case of my friends loving the ocean, the entire domain is covered, and generality achieved, in the sense that each name has a fixed interpretation in the calculus.

* *

This requirement is met in the case of the natural numbers

• 0, 1, 2, …

through the Omega operation, which supplies an explicit and fixed symbolic interpretation to fulfil the concept of ordinality. In later writings, for example in the Philosophical Grammar, on page 268, Wittgenstein will testify that, when he used the ellipsis in the Tractatus, he meant that he had not enumerated all the cases here but that they could be enumerated. To say that a series is denumerable is to say that all the members can be put on a single list. Not every series is denumerable, but the Omega series is:

• x, Ω'x, Ω'Ω'x, ... (6.02).

We can now state the general form of the Omega series:

• [x, ξ, Ω'ξ]=[ξ, Ω'ξ]'(x).

Anna is an instance of this general form. Actually, truth-functional logic is not the only instance of the Omega operation in the Tractatus. Another use is in the analysis of the natural numbers.

How does an operation effectively produce the series of natural numbers? The notion of iteration gives the Omega series. Wittgenstein does not assume the natural numbers, nor that the Omega series is fundamentally mathematical, for that would be anathema to his position. The natural numbers in the Tractatus are properties, not of logic, but of the operation. They are marks of mathematical concepts. Let me show you how.

Wittgenstein provides a recursive definition of the natural numbers using these symbolic rules:

• x=Ω⁰'x
• Ω'Ω^v'x=Ω^v+1'x.

The identity sign here indicates a purely stipulative assignation. With these stipulations the Omega series can be rewritten as:

• Ω⁰'x, Ω⁰⁺¹'x, Ω⁰⁺¹⁺¹'x, ...

Wittgenstein then simplifies the exponents using the following list of stipulations:

• 0+1=1,
• 0+1+1=2,

and so on.

This would give

• Ω⁰'x, Ω¹'x, Ω²'x

So the natural numbers turn out to be exponents. Let's check to make sure that works. For 0, we have stipulated that the first member of this series is the first member of the Omega series rewritten. Next, we verify the case for any successor ordinal:

That completes my reconstruction of section 6.02. Wittgenstein forthrightly declares that a natural "number is the exponent of an operation" (6.021). That is how Wittgenstein uses the Omega series to get the natural numbers. The general form of the natural numbers is:

• [0, ξ, ξ+1]=[ξ, ξ+1]'(0) (6.03).

I conclude this stage of the argument with three minor points concerning this analysis. First, truth tables, even the logical propositions themselves, are strictly superfluous (6.1203-6.1221). Second, truth does not apply to the equations of mathematics in the Tractatus, for these are pseudo-propositions (6.2). To maintain the consistency of this position requires that there be no dependence on a completed actually infinite series.³ Third, Wittgenstein does not appeal to mathematical intuition (6.2331).

* * *

The Omega series as Wittgenstein presents it leads to at least these two positive outcomes of his philosophy, which I summarize as slogans: First, that the a priori is all analytic; second, that a philosophical analysis of elementary arithmetic does not require a purely conceptual basis in logic. The Omega operation is the characteristic of Wittgenstein's philosophy that marks it as different from the philosophies of Frege and Russell. Logical atomism, if it is to have any significance at all, surely requires a logical analysis of elementary arithmetic. Among the many versions of logicism, the narrowest one, the core logicist position, is the position that elementary arithmetic is part of logic. If we accept this as a minimal case for logicism, then there is not so much to distinguish logicism from logical atomism in terms of Wittgenstein's approach. That suggests a difference in name only. As Juliet says,

a Rose
By any other name would smell as sweet.

Now granting that logical atomism encompasses this much of logicism, I shall complete my argument.

Suppose, for an argument by reductio ad absurdum, that Wittgenstein were a minimal logicist in the Tractatus. Then the notions of series, of succession, of first element, of next element, of the general laws of addition and multiplication, and of the natural numbers, would all be part of logic. Of course, in the Tractatus, addition, multiplication, and the tautology are provided for by the operation. Identity is not. Equations, then, are not part of logic. Wittgenstein cannot have meant that the tautology would explicate the concept of identity, and indeed that is exactly what he says in his letter to Ramsey.⁴ Identity is not a logical relation for Wittgenstein. But imagine it were. Such an account would still call for a conceptual analysis of number; Wittgenstein, however, never provides a conceptual basis in logic. Instead, he defines the natural numbers as exponents of an operation.

This is surprisingly close to anthropologism. Wittgenstein's main line can now be summarized. In the Tractatus Wittgenstein provides a case to refute logicism, a case in which at least some of elementary arithmetic is perfectly clear, absolutely in order, yet not logicistic.

Let me step back for a moment to consider a separate interpretative question much discussed during the past decade. Wittgenstein features the to and fro of philosophy (6.53), but the only way he can make his case against the logicism of Frege and Russell is by generating a positive and constructive account of (at least some of) elementary arithmetic with no logical concepts in play. I think he accomplishes this under an ideal assumption.

The mathematization of logic does not extend the realm of logic on Wittgenstein's view. This I believe sets a major interpretative hurdle for those who plump for Wittgenstein's logical atomism. The philosophical analysis that Wittgenstein actually carries out is logical but there is no basis in logic provided. The logic is to provide only the pure structure, like crystal.

The Omega series, a bare outline of pure form, realizes an ideal for logic, which explains why "logic is transcendental" in the Tractatus (6.13). This ideal for Wittgenstein at that time was sub specie humanitatis, within the realm of what is human.^†

Refbacks

• There are currently no refbacks.