From the ALWS archives: A selection of papers from the International Wittgenstein Symposia in Kirchberg am Wechsel

1. Introduction

There is a well known story about Victor Hugo who after having submitted Les miserables to his editor, went on holiday. He was anxious to know about its reception however, and sent the editor a telegram with the single sign “?”. Shortly thereafter he received the response “!” from the editor (Gion 1989). Clearly both telegrams carried a meaning for the receivers. The reason was the existence of the common context determined by the particular situation in which the messages could be interpreted.

The story exemplifies the difference between data and information and how sufficient background knowledge makes it possible to interpret data and turn them into information. The background knowledge defines a context in which to interpret the data. There are two mechanisms for this, either the condition of coherence imposes an interpretation or the context already contain definitions of the data. In any case, the story indicates that if the context is rich then the amount of data needed to describe a state of affairs is smaller than if the context is poor. It thus gives a clue to a preliminary definition of reduction with respect to context: a reduction of a context is an enrichment of the context.

In a formal linguistic setting a context is represented by an ontology, i.e. a set of implicit definitions of the words of the vocabulary used to describe the domain in question. The ontology provides the formal language with a semantic structure that pictures structural properties of its domain of application. The ontology in itself does not furnish the language with a full semantic. It must be supplemented by an interpretation that relates some of terms of the ontology to external ‘objects’, i.e. objects of its domain of application. The other terms are then given meaning by the definitions. A choice of terms whose interpretation is a sufficient basis for the semantic of a language are said to be primary. All the other terms are defined by the primary terms by means of the definitions. The definitions that only contain primary terms are called axioms (Blanché 1999). An ontology can thus be considered to be constituted by an axiom system or axiomatic core providing implicit definitions of the primary terms and a set of terminological definitions of the additional vocabulary.

An axiom system for the ontology resumes the syntactic and semantic information in the ontology. It is minimal with respect to both. The syntactic structure represented in the axiom system permits the deduction of all the theorems of the theory and the interpretation of the primary terms gives meaning to the terms introduced by the terminological definitions.

The language is used to describe objects or systems of the domain. The data necessary for a complete description of a system depends on the information content of the axiom system of the ontology. An extension of the system and thus of the ontology provides more information. Accordingly, an extension of the axiomatic system is a formal expression for reduction.

There are two kinds of reductions, ontological and theoretical reduction. Examples of both will be discussed in the following, however, limited to the case of formal scientific languages. By formal I will mean a language whose syntax is provided by first order predicate logic.

2. Structure of a formal scientific language

Any exposition of the structure of scientific theories is based on a number of distinctions representing ontological commitments. Those I have chosen are partly exhibited in the following figure:


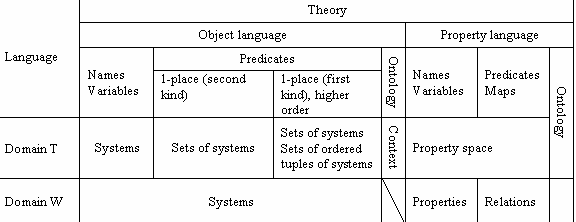
Figure 1
Here Domain W and Domain T stand for two different perceptions of reality; the Domain W corresponds to logical atomism and Domain T to the more elaborate set theoretical conception. The Figure 1 does not fully represent the relations between Language and Domain. It must complemented by the following diagram,


Figure 2
expressing the two interpretations of the correspondence between the structure of language and the reality: that the structure of reality is projected onto language or that the structure of language is projected onto reality. These interpretations are reflected in Wittgenstein’s (Wittgenstein 1961) and Tarski’s (Tarski 1944, 1985) semantic theories respectively: Wittgenstein’s semantic is represented by maps from the domain to language, while the Tarskian semantic is defined by a map from the language to the domain.

In a science there is a need to quantify over systems and properties, however, not both at the same time. Thus, the a priori second order language is naturally represented by a juxtaposition of two first order languages, the Object Language (OL) and the Property Language (PL). OL serves to give empirical descriptions of the systems of the domain and PL serves to describe the properties of the systems and to formulate models of systems. They are both endowed with semantic structures defined by ontologies. Their vocabularies consist of the logical constants and three kinds of terms, the names, variables and predicates, each kind having a particular syntactic role. A name refers to a unique system or property, a predicate to a property (predicate of the first kind) or a category of systems or properties (predicate of the second kind), or a relation between systems or properties. A variable refers to any of the elements in a given category. There is no syntactic difference between predicates of the first and second kind; the distinction is semantic. It is based on the ontological distinction between system and properties. A system is observed and thus conceived as a bundle of properties possessed by the system (bundle theory of substance).

The distinction between the two languages captures scientific practises. In OL the systems are directly referred to, while in PL the reference is indirect; it is given by means of identifying properties that are possessed by the system. Thus, while in OL Newton’s second law is expressed by

    the acceleration of a body equals the net force acting on the body divided by its mass

in PL the same law is represented by the mathematical formula

    a = F/m

which is without any explicit reference to the body. “Body” is not a term in PL. The body in question is implicitly referred to by the mass m that denotes a property of the body (system).

Figure 1 indicates that the set of properties/relations is represented by an abstract property space in the PL. In this language the relation between the property space and the names of the properties are also included. They are represented by maps that simulate the observation of properties. For example, the set of possible locations in real space is represented by the points of abstract three dimensional Euclidean space and the names of the points by their co-ordinates. This relation is formally represented by a map that relates the points of the abstract space with their co-ordinates. The ontology of the property language incorporates these relations. In the property language it is thus also possible to simulate the act of observation.

A model of a system is a representation of the system in the property language. From the model we can extract a description of the system modelled. The degree of correspondence between the empirical description in the object language and the theoretical description in the property language determines the correctness of the model.

3. Object language and ontological reduction

A domain consists of a set of (physical) systems that possess properties and relations. A system is uniquely identified and described by the properties it possesses. This is done by means of the atomic sentences that attach properties to the system, i.e. they are concatenations of the name of the system and the predicates that refer to the properties of the system. The basis for such a description is logical atomism. Each atomic sentence stands for an atomic fact. The conjunction of atomic sentences that applies to a system provides a description or picture of the system and serves to distinguish it from the descriptions of other systems.

Some properties are mutually exclusive in the sense that they cannot simultaneously be possessed by a given system; for example, a system cannot at the same time be red and green. This relation of exclusiveness of properties serves to categorise the predicates of the first kind. Each such category is then the range of a map from the set of systems of the domain to the predicates of the first kind. The map, called an observable, relates systems to the predicates denoting properties. Colour is thus an observable. Other examples of observables are form, temperature, position in space, mass, velocity etc.

One distinguishes between two kinds of observables referring to two kinds of properties, properties that do not change in time and thus serves to identify the system, and properties that change. The corresponding observables are identification and state observables respectively. The state properties form a space called the state space of the systems.

The systems can be classified with respect to the identification observables. One starts with one of the observables and uses its values to distinguish between the systems to construct classes. Thus, one gets a class for each value of the observable, the class of systems that possess the particular property, e.g. the class of all red systems, the class of all green systems etc. The procedure can be continued recursively until the set of identification observables is exhausted. The result is a hierarchy of classes with respect to the set inclusion relation. The basic entities of the classification are the elements of the leaf classes. The discovery of new independent observables will then lead to a refined classification and create new leaf classes and thus new classes of basic entities.

The classes are referred to by predicates of the second kind which thus are ordered naturally in a taxonomy that constitute a linguistic representation of the classification. The taxonomy together with the definitions of the classes is an ontology for the object language. The class definitions impose a semantic structure that mirrors the class inclusion relations and create semantic relations between the predicates. An extension of an ontology due to a refined classification is thus an example of an ontological reduction. Moreover, the domain of application of the new language is extended to incorporate the new systems to which some properties of the old systems can be referred. The axiom system for the ontology is given by the definitions of the leaf classes.

An example of a classification is that of material substances. They can be classified in terms of their chemical properties. In particular, the pure chemical elements are given by the periodic table. Taking into account the physical properties however, we get a refined classification distinguishing between isotopes of the same kinds of atoms.

The classification hierarchy can be given a mereological interpretation, i.e. the elements of the different classes may be identified by their composition in terms of elementary constituents (Smith et al. 1994). The passage from one level of granularity in terms of elementary constituents to a finer one which in the example above going from the atoms of the periodic table to the constituents of atoms (electrons, protons and neutrons) is an example of ontological reduction.

4. Property language and theoretical reduction

Physics offers many examples of theoretical reduction. We will consider one from classical mechanics. It has several equivalent formulations of which we will discuss two, the Newtonian and Hamiltonian mechanics.

The structure of Newtonian mechanics is defined by a set of axioms covering

• Euclidean space and time (abstract)
• Action of the Galilei group
• Operational definitions of velocity, length and time measures determining coordinatisations
• Calculus
• Newton’s second and third laws

The set of axioms supplemented with terminological definitions constitute an ontology for the property language of Newtonian mechanics.

A model is defined by the specification of a set of equations, the equations of motion. The equations of motion implement Newton’s second law and include quantities representing the identification properties of the system modelled and empirical constants, i.e. the masses of the objects and the gravitational constant. The solutions, moreover, depend on another set of empirical quantities defining initial conditions.

Hamiltonian mechanics is a formulation of classical mechanics that is a more restrictive way of looking at classical mechanics. It is based on the following elements

• Phase space and time as a differential manifold
• Action of Galilei group
• Operational definitions of momentum, length and time determining coordinatisations
• Hamilton’s principle of least action

The set of axioms supplemented with terminological definitions constitute an ontology for the property language of Hamiltonian mechanics.

A model of a system is defined by a function on phase space, the Hamiltonian, which includes reference to identification properties of the system modelled. Given the Hamiltonian, the equations of motion are derived from the hypothesis that the dynamics satisfies Hamilton’s principle.

The passage from Newtonian mechanics to Hamiltonian mechanics is a theoretical reduction; the axioms of Hamiltonian mechanics impose more structure than those of Newtonian mechanics but at the same time they define a more restrictive theory. The definition of a model is thus more compressed in Hamiltonian mechanics than in Newtonian mechanics. In fact, while the definition of a model of a simple system needs the specification of three functions, the force, in Newtonian mechanics, it is defined by only one function, the energy, in Hamiltonian mechanics. The domain of application of Hamiltonian mechanics is however, smaller than that of Newtonian mechanics. In fact, while Newtonian mechanics can model dissipative systems, Hamiltonian mechanics can only handle conservative systems.

It should be noticed that the terms reduction is also used to denote the limit of physical theories for parameters going to zero.