Abstract
The picture theory from Wittgenstein’s Tractatus logico-philosophicus provides a correspondence principle for the semantics of a formal language that in contrast to Tarski’s extensional interpretation scheme, can be represented by maps from the domain to the language. It makes possible intensional interpretations of the predicates of the language of discourse for a domain consisting of physical objects or systems. The aim of this paper is to outline the basis for such an interpretation and explain how it can be extended to a language of discourse for the properties of the physical systems.
Table of contents
The picture theory from Wittgenstein’s Tractatus logico-philosophicus provides a correspondence principle for the semantics of a formal language that in contrast to Tarski’s extensional interpretation scheme, can be represented by maps from the domain to the language. It makes possible intensional interpretations of the predicates of the language of discourse for a domain consisting of physical objects or systems. The aim of this paper is to outline the basis for such an interpretation and explain how it can be extended to a language of discourse for the properties of the physical systems.
1. Introduction
A first order formal language has of the following elements:
- Vocabulary
- - Names, Variables, Predicates
- - Logical constants
- Rules of syntax
- Sentences and formulae
- Logical axioms
- Rules of deduction
- Ontology
- - Axioms
- - Terminological definitions
- Interpretation (semantics)
The vocabulary consists of words with different syntactic roles and semantic values that are used to formulate sentences and formulae according to the syntactic rules. The logical axioms limit the scope of the logical constants, while the ontology axioms both provides the language with a semantic structure by being implicit definitions of the primary terms of the vocabulary and a model of the domain picturing its structural properties. Secondary terms that serve to facilitate the discourse are introduced by terminological definitions.
Excluding the interpretation we are left with a formal system, i.e. a formal language is a formal system supplied with an interpretation. The interpretation is relating the primary terms of the vocabulary to external ‘objects and actions’.
The standard way of providing a formal language with an interpretation is extensional and due to Tarski (1983, ch. VIII). If the domain of discourse consists of a set of (physical) systems, then a name denotes an individual system, a one-place predicate denotes a set of systems to which the predicate apply, a two-place predicate the set of pairs of ordered systems to which the predicate apply etc. The semantics is thus defined by a map that maps the names to the individual systems and the predicates to the set consisting of sets of individuals, sets of ordered pairs of individuals etc.
Russel’s antinomy highlighted a problem threatening extensional interpretations. To avoid this problem at the outset Wittgenstein (1961) in Tractatus introduces the picture theory as a basis for the interpretation by correspondence with respect to the metaphysical assumption of logical atomism. A picture of a system can be seen as the image of a map from the domain to the language. I will use this to outline a scheme for intensional interpretations of scientific theories in the framework of first order languages.
The restriction to first order makes it necessary to decompose the language in two coupled first order languages, an object language in which to describe the empirical facts about the systems of the domain and a property language in which to describe the properties of systems (Aaberge 2007). The reason for this separation is the need to quantify over physical systems and properties alike, but not in the same propositions. The distinction between the two languages captures scientific practice. In the object language a system is directly referred to, while in the property language the reference is indirect; it is given by means of identifying properties that are possessed by the system. The distinction is exemplified by the sentences “the water in bottle 3 is 5°C” and “5°C is a temperature” in the object and property language respectively. Here 5°C is a predicate of the first kind in the object language and a name in the property language.
2. The object language
Observations, operational definitions and observables
The object language applies to a domain consisting of physical systems. Physical systems possess properties and the attribution of a property to an individual system constitutes an atomic fact about the system. It is expressed by an atomic proposition, i.e. true atomic propositions are statements about observed atomic facts. The observations of atomic facts all involve the use of a standard of measure. The result of an observation follows from a comparison between a representation of the standard and the system. It determines a value from the standard, a predicate of the first kind.
Observations/measurements are based on operational definitions, i.e. definitions that specify the applied standard of measure, the laws/rules on which the measurements are based and the instruction of the actions to be performed to make a measurement. The operational definitions are formulated in a separate language. They provide intensional interpretations of the predicates expressing results of observations. The measurement of the colour of a system is an example. The measuring device is then a colour chart where each of the colours is named and the rule of application is to compare the colour of the system with the colours on the colour chart and pick out the one identical to the colour of the system. The name of the colour picked denotes the result of the measurement.
Each operational definition is symbolised by an observable that simulates the act of observation; the observable is an injective map between the domain and the set of predicates (of the first kind) that maps a system to the predicate representing a property possessed by the system (Piron 1975). The set of possible values of an observable represent mutually exclusive properties of the systems of the domain; no two properties corresponding to different values of the same observable can be possessed by any system. A system cannot at the same time weight 1 kg and 2 kg. Weight is therefore an observable. Other examples of observables are position in space, number of systems in a given container and colour of systems.
Names, predicates of the first kind and truth
Let L(D;N∪V,P1∪P2 stand for the object language for a domain D. N denotes the set of names, V the set of variables, P1 the set of predicates of the first kind and P2 the set of predicates of the second kind1. The distinction between predicates of the first and second kind is semantic and made possible by the intensional interpretation. The names of the systems are given by a map ν,
ν:D→N; d↦ν(d)
that to a system d in the domain D associates the name n by ν(d) = n . ν is an isomorphism; by convention, there is a unique name for every system and there is exactly the same number of names and systems.
Each observable δ determines an atomic fact about a system d∊D by
δ:D→P1; d↦δ(d)
For each δ there exists a unique (injective) map π defined by the condition of commutativity of the diagram

The diagram relates the simulation of measurements determining atomic facts assigning a property to a system and the formulation of an atomic sentence expressing such a fact by the juxtaposition pn of the name n referring to the system d and the predicate p referring to the property, i.e. if π(ν(d))=δ(d), for ν(d)=n and π(n) =p. The commutativity condition π(ν(d))=δ(d) is thus the truth condition of the object language. It equates a proposition about the system d with a statement of the result of a measurement on d with respect to the observable δ.
The Tarski interpretation can be derived from the above interpretation. By taking the inverse images of the predicates of the first kind with respect to the observables we get the extensions of the predicates. The opposite is however, not the case. The reason is that intensional definitions contain much more information than extensional enumerations. In particular, operational definitions give meaning to predicates of the first kind at the outset while those of the second kind are introduced by terminological definitions.
Predicates of the second kind
One distinguishes between two kinds of observables referring to two kinds of properties, properties that do not change in time and thus serves to identify the system, and properties that change. The corresponding observables are identification and state observables respectively.
The systems can be classified with respect to the identification observables. One starts with one of the observables and uses its values to distinguish between the systems to construct classes. Thus, one gets a class for each value of the observable, the class of systems that possess the particular property, e.g. the class of all red systems, the class of all green systems etc. The procedure can be continued recursively until the set of identification observables is exhausted. The result is a hierarchy of classes with respect to the set inclusion relation. The basic entities of the classification are the leaf classes.
The classes are referred to by predicates of the second kind which thus are ordered naturally in a taxonomy that constitutes a linguistic representation of the classification. The satisfaction conditions defining the classes are intensional definitions of the predicates of the second kind. They are of the form
- pn1 = p1n1 ∧ p2n1 ∧ ... ∧ pmn1
- pn2 = p1n2 ∧ p2n2 ∧ ... ∧ pmn2
- ∙
- ∙
- pnk = p1nk ∧ p2nk ∧ ... ∧ pmnk
where p is the predicate of the second kind referring to the class defined by the satisfaction condition, p1, p2, p3, … pm are the values of the different observables and n1, n2, … nk, stand for the names of the systems for which the atomic propositions are true. The set of intensional definitions constitute terminological definitions belonging to the ontology of the language.
In the framework of the property language the subject-predicate form of the atomic propositions whose function is to attribute a property to a system can be considered fundamental. Seemingly atomic propositions like “pn” where p is a predicate of the second kind are only abbreviations of sentences being conjunctions of atomic sentences. For example the sentence “S-2003 is a Car” hides the description of what falls under the concept referred to by the predicate of the second kind “Car”.
3. Property Languages
Properties
Predicates of the first kind refer to properties of systems. A property is something in terms of which a system manifests itself and is observed, and by means of which it is characterised and identified. To an observer a system appears as a collection of properties. The properties of a system are thus in a natural way mentally separated from the system. The separation is made possible by the fact that the ‘same’ property is possessed by more than one system. It is expressed by the commutativity of the following diagrams

where E is the abstract representation of the set of properties of the systems in D; the ε are injective maps that simulates the ‘mental’ separation of properties from the systems. In the case of coloured systems for example, the condition of commutativity means that if a system appears as red then it possesses the property redness. It is assumed that each predicate of the first kind refers to a unique potential property.
The property space E is a construction characterised by the diagram. The E chosen is a natural extension of the set of properties that can be associated to the systems of the domain as reflected in the set of predicates available in the standards of the operational definitions..
The maps ρ:E→P1; e ↦ ρ(e) can be considered as naming maps for the properties, e.g. a point in abstract space is named by a set of coordinates. To describe the properties we need a formal language, the property language L(E,P1∪W,Q), were P1 denotes the set of names, W the set of variables and Q the set of predicates. The property language is associated with the diagrams
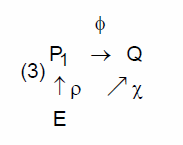
The symbolic entities of E also belong to the property language. The maps ρ thus symbolises the kinds of measurements inside the language.
Ontologies
The ontology of the property language is a set of definitions relating the terms of the vocabulary. It consists of an axiom system giving implicit definitions of what is chosen to be the primary terms and a set of terminological definitions introducing secondary terms which serves to simplify the discourse. The axioms are formalised accounts of the operational definitions which constitute a basis for the interpretation of the primary terms. The axioms define a semantic structure that pictures structural properties of the domain as seen through the operational definitions (Blanché 1999).
The Theory of Special Relativity offers an example for how operational definitions impose an axiomatic structure on the property language. It is derived from an operational definition of time and distance measurements based on a definition of simultaneity of distant events with respect to a given observer, the physical law claiming the velocity of light to be constant and independent of the velocity of the emitting source and the Principle of Relativity which postulates that the laws of physics are the same in all inertial frames of reference. Presently, the standard unit of time defines the second to be 9 192 631 770 periods of the radiation emitted from the transition between two hyperfine levels in the ground state of Caesium 133. Moreover, 1 meter is equal to the distance covered by a light ray in empty space in 1/299 792 458 seconds. Length measurements are thus based on time measurements.
The axioms of the property language express the content of the operational definitions which constitute the basis for empirical investigations. Their truth can therefore not be ascertained through empirical investigations. They are “hinge” propositions expressing statements about structural properties of the property language that reflects structural properties of the domain as seen through the “lenses” of the operational definitions (Wittgenstein 1975). The object language can only be indirectly tested by means of the models of systems of the domain formulated in the language.
4. Theories
A theory for a given domain is the juxtaposition of an object language and a property language. Because of their association the triples of observables δ, π and ρ constitute the bridges between the object language and the property language with the observables δ as the central parts. The diagrams
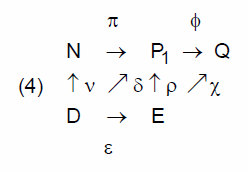
i.e. the composition of the diagrams (1), (2) and (3), expresses the structure of a scientific theory.
The commutativity of the diagrams (1) and (2) defines a unique π and ρ for each δ and ε. They all express the attribution of a property to a system and therefore represents the act of measurements. They will all be referred to as observables. Though their function differs the observables in a triple are therefore also given the same name. Colour is an example. Thus, while δ, by
δ(d)=red associates the colour red to a system d,
π(n)=red stands for the atomic proposition “n is red”,
ε(d)=redness claims that the system possesses the
property redness and ρ(redness )=red gives the name to the property. The observation that a system is red expressed by the sentence “n is red” is therefore to be interpreted as expressing that the system whose name is n possesses the property redness. This interpretation is justified by the commutativity of the diagram (4). The diagram thus shows how the semantic of the property language is based on the operational definitions.
5. Concluding Remarks
When Wittgenstein returned to philosophy in 1929 he started with the intention to revise Tractatus logico-philosophicus. He had become aware of its shortcomings as regards some of his initial objectives. In particular, he had discovered that the symbolism of Tractatus, the truth-false notation, did not exclude the construction of nonsensical sentences like “x is red and x is green” (Marion 1998). This forced him to abandon one of the pillars of Tractatus, the thesis that atomic sentences are independent (Tractatus 5.134).
I have made two proposals that make it possible to avoid some of Wittgenstein’s own objections to the Tractatus. I have considered the language of discourse for a scientific domain to be the juxtaposition of two separate but interdependent languages; moreover, the definition of the observable by mutual exclusiveness imposes a restriction on the syntax that goes outside the purely truth functional logic. It implies that sentences like “p1n∧p2n”, where p1 and p2 are different predicates of the first kind belonging to the same observable, are necessarily false since at least one of the atomic sentences in the conjunction must be false.
The realisation that there are constructions in language, outside the scope of truth-functional logic forced Wittgenstein to extend his investigations. He started to look at the different functions of natural language and introduced the notion of language game to account for its semantic foundation. Language is correctly applied if the discourse satisfies the rules of the game (Wittgenstein 1968).
In a language of the kind I am proposing, there are different kinds of rules that fall under the category of language game, the syntactic rules, deduction rules and the rules that the axioms of the property language imposes on the application of the primary terms. In addition, there are meta rules imposed by the operational definitions determining the interpretation of the primary terms as well as meta rules determining the semantics of the property language. It is clear that these different rules are at least partly interdependent. This interdependency should be analysable along the lines of Investigations and On Certainty.
I hope to have shown that a coherent intensional interpretation can be made of the framework of a scientific theory. To make a comprehensive extensional interpretation seems however, to be more difficult if at all possible because the underlying conceptual model of the domain and the direction of the interpretation map does not allow for the construction of commutative diagrams.
Literature
- Aaberge, Terje 2008 : The 31st International Wittgenstein Symposium
- Blanché, Robert 1999: L’axiomatique. Paris: Presses Universitaires de France
- Marion, Mathieu 1998: Wittgenstein, Finitism, and the Foundations of Mathematics. Oxford: Clarendon Press
- Piron, Constantin 1975:Foundations of Quantum Physics. Boston: Benjamin Inc.
- Tarski, Alfred 1983: Logics, Semantics, Metamatematics. Indianapolis: HackettPublishing Company, Inc.
- Wittgenstein, Ludwig 1961: Tractatus logico-philosophicus. London: Routledge and Kegan Paul
- Wittgenstein, Ludwig 1968: Philosophical Investigations. Oxford: Blackwell Publishers Ltd.
- Wittgenstein, Ludwig 1975: On Certainty. Oxford: Blackwell Publishers Ltd.
Refbacks
- There are currently no refbacks.