From the ALWS archives: A selection of papers from the International Wittgenstein Symposia in Kirchberg am Wechsel

1. Introduction

The domain of discourse for a language is assumed to consist of individual objects possessing properties and relations. The attribution of a property to an individual or a relation to a pair of individuals is an atomic fact expressed by an atomic sentence. There are two ways of conceiving the relation between language and domain; either that the structure of the domain is mapped into the language or that the structure of the language is mapped into the domain. The first of these corresponds to Wittgenstein’s picture theory in Tractatus [1961] the second one is attributed to Tarski [1983] being the standard view in semantics of first order formal languages.

The conceptualisation of the structure of a domain is related to the choice of direction of the map(s). In the first case the domain is modelled as a directed graph. An individual is then represented by a node and a relation by an arrow; in the second case it is modelled as a set consisting of individuals, sets of individuals, sets of ordered pairs of individuals etc. These conceptualisations are the basis for the intensional and extensional interpretations respectively. The intensional interpretations are represented by maps, a naming map that maps the individuals (or relations) to names and observables that map an individual (or relation) to a predicate representing a property (or relation). The extensional interpretations are represented by a map that maps names to the individuals, a one-place predicates to the set of individuals possessing the property referred to by the predicate, a two-place predicate to the set of ordered pairs of individuals possessing the relation denoted by the predicate etc.

The notion of observable is a fundamental building block in the intensional interpretation scheme. An observable is simulating a kind of measurements the results of which are predicates representing properties of individuals or relations between individuals. It simulates the act of measurement and is associated with an operational definition, i.e. the specification of a standard of measure, laws on which the measurement is based and rules determining the actions to be performed to make the measurement. The possible values (predicates) of an observable represent mutual exclusive properties of individuals or relations between two individuals. Individuals can not be red and green at the same time. Thus colour is an observable. Other observables are temperature, weight, position in space etc.

The result of a measurement on an individual or relation is expressed by a predicate and stated by a sentence that relates the name of the individual or individuals partaking in the relation. These are the atomic sentences of the language. The truth conditions are therefore particularly simple. An atomic sentence is true iff it states the result of a measurement. This is expressed in the model of the domain of the metalanguage by a set of commutative diagrams [Aaberge 2009a]

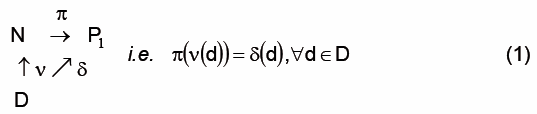
where D denotes the domain, N the names, P the predicates, ν is the naming map δ is an observable and π is defined by the commutativity of a diagram.

2. The metalanguage

Let L_D(N∪N⁽²⁾∪V,P₁∪P⁽²⁾∪P₂ stand for the object language for a domain D, i.e. the set of names, predicates, variables and sentences. N∪N⁽²⁾ denotes the set of names, V the set of variables, P₁ the set of predicates of the first kind, P⁽²⁾ the set of two-place predicates and P₂ the set of predicates of the second kind.

The metalanguage for the object language is denoted L_G(M₁∪M⁽²⁾,Q where the domain G consists of the set D∪L_D(N∪N⁽²⁾∪V,P₁∪P⁽²⁾∪P₂) endowed with the directed multi-graph structure defined by the diagrams (1), M₁ = D∪L_D(N∪N⁽²⁾∪V,P₁∪P⁽²⁾∪P₂ the names¹ of the nodes, M⁽²⁾ the names of the relations q (arrows d↦n etc. in (1)) and Q the predicates of the metalanguage. In the metalanguage D represents the symbolic model of the domain.

The names of the individuals, relations between individuals, terms, sentences and relations between these objects in the metalanguage, are given by the naming map

where ν(d)=n denotes relations (arrows: d ↦n ) etc.
Each observable α determines an atomic fact about an element of the domain G,

α:G→Q;g↦α(g) (3)

Moreover, for each observable α there exists a unique map β defined by the condition of commutativity of the diagram

An observable σ, the semantic observable, has the values² D, D⁽²⁾, N, N⁽²⁾, V, P, P⁽²⁾, S, H, P_ν, P_π, P_π(2), P_δ, P_δ(2)

informally defined by³

• 1. Dm, m is an individual
• 2. D⁽²⁾m, m is a relation
• 3. Nm, m is the name of an individual
• 4. N⁽²⁾m , m is the name of a relation
• 5. Vm, m is a variable
• 6. Pm, m is a 1-ary predicate
• 7. P⁽²⁾m , m is a 2-ary predicate
• 8. Sm, m is a sentence
• 9. Hm, m is a formula
• 10. P_νm₁m₂, m₁ is named m₂
• 11. P_πm₁m₂ ,m₁ is m₂
• 12. P_π(2)m₁m₂, m₁ is m₂
• 13. P_δm₁m₂ , m₁ possesses the property represented to by m₂
• 14. P_δ(2)m₁m₂ , m₁ is the relation represented by m₂

The operational definition is given by the syntactic rules and interpretation of the language and the semantic value of a symbol are determined by inspection. It should be noticed that these predicates of can serve to characterise names and terms of the object language and thus makes possible a map that to an sentence associates a syntactic description of the sentence. The metalanguage might thus serve as the basis for the construction of an ontology language.

Syntactic rules and rules of deduction are formulated in a metalanguage. The syntactic rules are of the form

atomic sentence: Nn ∧ Pp ⇒ Spn

conjunction: Hf₁ ∧ Hf₂ ⇒ H(f₁ ∧ f₂)

univer. quant.: Hf(x) ⇒ S (∀_xf(x))

etc.

The rules of deduction, modus ponens and generalisation are in the notation introduced expressed by [8]

modus ponens: Tf₁ ∧ T(f₁ ⇒ f₂)) ⇒ Tf₂ (6)

generalisation: if it is assumed that the hypotheses underlying the derivation of f(x) does not depend on x then

(Hf(x)) ⇒ T ∀_x f(x)

The metalanguage is endowed with an ontology that provides implicit definitions of the terms of the vocabularies and at the same time pictures structural properties of the respective domains. It is defined by the axioms which summarise the content of the commutativity conditions (1):

Axiom: for each of the diagrams the commutativity conditions (1, 7) hold for an atomic sentence iff the sentence is true, i.e.

Dm₁ ⇒ Nm₂ ⇒ P₁m₃ ⇒ (P_νm₁m₂ ⇒ P_δm₁m₃ ⇒ P_πm₂m₃)) (7)

and similarly for the relations.

Whether an atomic sentence is true or false can be ascertained by inspection using these axioms. The inspection involves making measurements.

This gives rise to another observable τ given by the values true T, neutral I or false F. τ is neutral for all individuals, relations, terms and formulae, and true or false on the sentences, i.e. if s is a sentence, then the truth of s is expressed by Ts.

3. Concluding Remarks

The intensional interpretation of an object language and construction of its meta-language is made in the spirit of Tractatus, being based on the picture theory. There are, moreover, no sets are involved, though an extensional interpretation can be obtained by taking the inverse image of a predicate by its observable as the extension of the predicate. Moreover, a verification procedure for atomic sentences has been given. To determine whether a predicate applies to an individual we make a measurement. It consists in comparing a property of the individual with the standard of measure. The comparison determines the property of the individual that is identical to the property of the standard of measure. The predicate denoting this property in the standard of measure then applies to the individual.

The standard of measure defining the values of an observable is picturing mutually exclusive potential properties of objects. For example, the numerical values on the scale of an old fashioned thermometer are picturing the temperatures of the mercury in the thermometer. The picture is based on the law of linear increase of volume with temperature within a certain temperature range limiting the validity of the thermometer as a measuring device. To measure the temperature of an object the thermometer is brought into contact with the object. According to the second law of thermodynamics after some time the thermometer and the object will be in thermal equilibrium. The thermometer then shows the common temperature of both objects. Comparison thus means the identification of pictures; in this case the comparison is intrinsic. The following example shows other aspects of how the comparison takes place. The measurement of the colour of an individual consists in holding a colour chart representing the standard of measure for the colours against the individual. If the mental pictures that the observer gets of the colour of the individual and the colour marked red on the colour chart coincide, then red is taken to denote the result of the measurement.

The intensional interpretation scheme realises the conception of Investigations (Wittgenstein 1968). In Investigations Wittgenstein analyses how language games are used to determine meaning of words by their application to a given context. In our case, the particular sets of operational definitions can be considered as constituting a language game and the corresponding acts of measurements the context which gives the basis for the intentional interpretation. How meaning depends on the operational definitions is illustrated by the operational definitions of time and distance measurements in non relativistic physics and special relativity. In non relativistic physics one distinguishes between the measurement of a distance in space and the duration in time. Distance is measured by a rod of unit length and duration by a periodic process; one counts the number of rods that is needed to cover the distance or the number of periods that is needed to span the duration.

In special relativity only a standard unit of time is defined. The unit of length is defined as the distance covered by a light ray in a given interval of time. The measurement of time is based on a definition of simultaneity of distant events with respect to a given observer, the physical law claiming the velocity of light to be constant in vacuum and independent of the velocity of the emitting source and the Principle of Relativity which postulates that the laws of physics are the same in all inertial frames of reference. Clearly, the measurements associated with these sets of operational definitions corresponds to different language games and thus give different meanings to the notions of duration and distance.

Operational definitions are practical implementations of the axioms of the property language for the domain considered. Accordingly, a property language (theory) can not be directly tested. It is indirectly tested by means of models of the individuals of the domain formulated in the property language [Aaberge 2009a]. As Wittgenstein points out in On Certainty (Wittgenstein 1975) we need a ground for asserting the result of an observation, i.e. for the result of a measurement on an individual to state something about the individual. As the above discussion shows the ground is in our case provided by the comparison with a standard and the identification of properties. This is what is expressed by the truth conditions (7). The reference to the measurements then give the meaning to the terms of the object language, property language and its metalanguage based on intentional interpretations. These three languages give a complete framework for the description of a domain. The structure of the metalanguage is here essential since it only contains the name of a sentence and not the sentence itself contrary to Tarski’s truth conditions ““s” is true iff s” (Tarski 1944) which gives rise to an infinite hierarchy of languages. The truth conditions expressed by the axioms (7) are closed statements.

The meaning of the terms of a language is partially fixed by an ontology modelling the context of a language game. Partakers in a language game may test their interpretation of terms used by judging it in the metalanguage applying modus ponens and thus slowly adapt to their meaning to be in accordance with the meaning fixed by the ontology.

The objects of the domain of the metalanguage are symbolic representatives of the individuals and relations of the object language (one cannot put the objects and relations themselves into the language), the names, predicates and sentences. The naming map and the observables in the diagram (1) then express kinds of semantic relations. Moreover, the diagrams generate a directed graph model of the domain G in which the sentences are isolated nodes. The model is given a linguistic representation by the primary vocabulary and the axiom system expressing the truth conditions. The atomic facts represented by the atomic sentences in the metalanguage do not have the same ontological status as the atomic facts represented by atomic sentences in the object language which concern the acts of measurement As shown by the example of time and space measurements their ontological status thus depends on the ontological status given to the laws used to interpret the results of the measurements and to the individuals of the domain.