From the ALWS archives: A selection of papers from the International Wittgenstein Symposia in Kirchberg am Wechsel

• Home
• About
• Login
• Search
• Current
• Archives

Table of contents

• Widmung
• Danksagung
• Literatur

Nichts geht heute ohne Computer, auch die wissenschaftliche Beschreibung der Welt nicht. Dabei produzieren diese Maschinen Sätze, die wahr und falsch sein können. Dieser Aufsatz weist nach, dass aus für uns unüberwindbaren technischen Gründen ein Großteil, ja vielleicht sogar alle diese Sätze ihren Wahrheitswert nicht allein der Welt verdanken, über die sie sprechen, sondern willkürlicher Festlegung. Ist angesichts dessen eine exakte Beschreibung der Welt mit maschinenlesbaren Sprachen möglich? Wir wollen dieser Frage mit einem Gedankenexperiment nachgehen. Um uns nicht in den Feinheiten der vielen maschinenlesbaren Sprachen zu verlieren, werden wir in der Umgangssprache bleiben und ein Merkmal der maschinenlesbaren Sprachen auf sie übertragen.

TND-Kriterium: Jeder Satz trifft entweder zu oder nicht, aber nicht beides.

„TND“ heißt dieses Kriterium, weil es an das aussagenlogische Gesetz des Tertium Non Datur erinnert. Es ist jedoch metasprachlich formuliert und passt darum auf viele Sprachen. Z.B. kommt „ApNp“ nur in einigen polnisch notierten aber nicht in allen maschinenlesbaren Sprachen vor.

Beginnen wir mit dem Experiment und stellen uns ein Zebra namens „Ziggy“ vor. Wir wollen entscheiden, ob der Satz „Ziggy ist schwarz” wahr ist. Einige Teile von Zebras sind schwarz und einige nicht. Wenn Ziggy schwarz ist, dann muss das etwas mit seinen schwarzen Teilen zu tun haben, denn sonst könnten auch Zitronen, die keine schwarzen Teile haben, schwarz sein.

Nehmen wir an, Dinge stimmen in allem mit ihren Teilen überein. Demnach wären Zebras schwarz, weil sie schwarze Teile haben und sie wären auch nicht schwarz, weil sie auch andere Teile haben. Ein Widerspruch! Nehmen wir deswegen an, Dinge stimmen in nichts mit ihren Teilen überein. Folglich wären Zebras, weil sie solche Teile haben, nicht schwarz. Weil sie aber auch Teile haben, die nicht schwarz sind und mit diesen nicht übereinstimmen sollen, müssen sie nicht nicht schwarz sein. Folglich sind sie schwarz. Ein Widerspruch! Widersprüche folgen nur aus Falschem. Die Annahmen, Dinge stimmen in allem bzw. sie stimmen in nichts mit ihren Teilen überein, sind darum falsch. Demzufolge stimmen Dinge in manchem mit ihren Teilen überein und in manchem auch nicht. Doch worin stimmen sie überein und worin nicht?

Gibt es eine Regel, die festlegt, welche Eigenarten Dinge von ihren Teilen erben und welche nicht? Michelangelos David ist aus Marmor. Er enthält aber auch Spuren anderer Mineralien wie z.B. Hämatit. Doch der größte Teil des David ist aus Marmor, weswegen wir das dem ganzen David auch zusprechen. Wir wenden also das Mehrheitsprinzip an. Doch wir bezeichnen ein Hemd mit nur einem Fleck, bei dem 99 % des Stoffes noch sauber sind, als schmutzig. Bei dem Hemd gilt das Mehrheitsprinzip nicht. Es gibt keine Regel, die sagt, ob ein Ding mit den Eigenarten seiner Teile übereinstimmt oder nicht.

Wir wollen die Dinge, die eine solche Regel benötigen, „zebrig“ nennen. Etwas ist also zebrig gdw. es verschiedene Teile hat. Verschieden sind die Dinge, auf die verschiedene Sätze zutreffen. Dahinter verbirgt sich das Ersetzbarkeitsprinzip nach Leibniz. So sind Schnee und Kohle verschieden, weil sich in dem wahren Satz „Schnee brennt nicht.“ „Schnee“ nicht durch „Kohle“ ersetzen lässt, ohne dass der entstehende Satz falsch wird.

Allgemein gesagt: Nehmen wir ein zebriges z an. Nun gibt es ein x und ein y, die seine Teile und verschieden sind. Es gibt also einen wahren Satz S aus dem ein falscher entsteht, wenn wir darin den Namen von x durch den von y ersetzen. Was uns fehlt, ist eine Regel, die bestimmt, ob der Satz wahr ist, der aus S entsteht, wenn wir den Namen von x durch den von z ersetzen.

Die Wahrheit eines solchen Satzes im Allgemeinen und „Ziggy ist schwarz“ im Speziellen können wir nicht logisch deduzieren oder empirisch entdecken, sondern müssen sie willkürlich festlegen. Je nachdem, wie wir wollen, ergeben sich verschiedene Beschreibungen von Ziggy. Dieses Problem, dass die Beschreibungen zebriger Dinge auch von Willkür abhängt, soll „Zebraproblem“ heißen. Das Zebraproblem betrifft nicht alle Sätze und alle Dinge, sondern nur das Aufeinandertreffen bestimmter Dinge und Sätze. Ein Teerklumpen hätte zwar auch Teile, aber eben nur schwarze, weswegen hier die Zuschreibung einfach ist. Eine Zitrone löst das Problem in Bezug auf die Schwärze auch nicht aus, weil sie überhaupt keine schwarzen Teile hat. Zebras, Schachbretter und die Seite dieses Textes lösen sie jedoch für die Schwärze aus.

Wir wollen uns das Zebraproblem bei echten maschinenlesbaren Sprachen am Beispiel einer primitiven Digitalkamera klar machen. Der Einfachheit halber wollen wir annehmen, die Kamera könnte nur schwarz und weiß abbilden. Das Argument wäre aber mit jeder anderen Zahl von Farben wiederholbar. Denn wesentlich ist, dass ein Pixel eine bestimmte Farbe hat oder nicht aber nicht beides. Auch wenn sie nicht so aussehen, Pixel sind Sätze. Was wir auf dem Display oder auf den Druckbogen sehen, ist nur eine Umsetzung eines Satzes. Im Rechner werden keine Bilder umhergewälzt, sondern Listen von Beschreibungsätzen. Eine Beschreibung von Ziggy im Dateiformat TIFF mit CCITT Codierung [Lipp 1997] könnte so aussehen:

• 0111 010 000111
• 10 000111
• 000111 010 000111 010

Wie ein normaler deutscher Satz kann eine solche Beschreibung auf das Abzubildende zutreffen oder nicht. Die Liste oben würde übrigens als die Pixelgrafik unten links in der Skizze angezeigt werden.

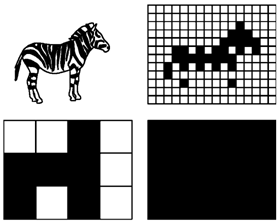Abb.: Ein Zebra als Pixelgrafik

Im Extremfall, z.B. bei einer sehr schlechten Kamera oder wenn das Zebra weit weg ist, steht für das ganze Zebra nur ein einziges Pixel zur Verfügung und wir haben das Zebraproblem in der besprochenen Form. In milderen Fällen tritt es nicht für das ganze Zebra, sondern nur Teile davon auf. Hier muss ein Pixel einen Teil des Zebras abbilden, das seinerseits zebrig ist, weil es z.B. weiße und schwarze Teile hat. Der vom Programmierer festgelegte Algorithmus in der Kamera muss entscheiden, wie dieses Pixel gefärbt wird. Das Aussehen des Bildes wird also nicht nur vom Zebra, sondern auch vom Programmierer bestimmt. Je nachdem, wie der Algorithmus aussieht, ergeben sich verschiedene Abbildungen desselben Gegenstandes.

Der kluge Programmierer wird deswegen so vorgehen, dass er einen Algorithmus schreibt, dann mit dessen Hilfe Bilder macht und diese mit dem Original vergleicht. Er wird die Regeln für die Farbzuweisung der Pixel im Algorithmus dabei zunehmend so verfeinern, dass das Bild einem Zebra immer ähnlicher wird.

Bedrohlich wird das Zebraproblem für wissenschaftliche Abbildungen. Denn hier kann das Bild meist nicht mit dem Abgebildeten verglichen werden. Das tiefste Innere der Zellen und die äußersten Weiten des Weltraums kennen wir nur noch aus Pixelgrafiken. Ein Vergleich der Bilder mit der direkten Anschauung der Dinge, die sie zeigen, ist nicht mehr möglich. Wir wissen so nicht einmal, ob ein zebriges Objekt abgebildet wurde oder nicht, weil das von Willkür geprägte Bild immer schon zwischen uns und den Dingen in der Welt steht. Der Biologe, der Zellen mit digitalen Bildern erforscht, ist in einer ähnlichen Lage wie ein Kollege, der Sonnenblumen nur auf Grundlage von van Goghs herrlichem aber sehr willkürlichem Gemälde erforschen würde. Er sieht den Gegenstand nicht mehr selbst, sondern nur noch dessen Gemälde und er kann nicht entscheiden, was daran van Gogh oder Natur ist.

Was hat Ludwig Wittgenstein mit all dem zu tun? In seinem Tractatus Logico-Philosophicus [Wittgenstein 1963] skizziert er eine das TND-Kriterium erfüllende Sprache und stellte eine Theorie auf, wie eine exakte Beschreibung der Welt mit so einer Sprache möglich sein soll.

Die Welt ist vollständig beschrieben durch die Angaben aller wahren
Elementarsätze, plus die Angabe welche von ihnen wahr sind. [TLP 4.26]

Mit „vollständig“ meint Wittgenstein, dass sich keine weiteren Informationen über die Welt geben lassen. Eine vollständige Beschreibung passt nur auf eine einzige Welt. Träfe sie auf zwei verschiedene Welten gleichermaßen zu, dann würde sie die Unterschiede zwischen diesen beiden Welten vernachlässigen und wäre damit nicht vollständig beschrieben. Vollständige Beschreibungen treffen also niemals auf mehrere verschiedene Dinge zugleich zu. Allgemein gesagt: Eine Satzmenge S ist eine vollständige Beschreibung von x gdw. es kein solches y, dass S einen falschen Satz enthält, wenn man in jedem ihrer Sätze den Namen von x durch den von y ersetzt.

Wir könnten uns vorstellen, S enthielte alle wahren und die Negationen alle falschen Elementarsätze. Dann wäre S nach Wittgenstein eine vollständige Beschreibung der Welt. Wie ermöglichen uns die Elementarsätze dies?

Ist der Elementarsatz wahr, so besteht der Sachverhalt, ist der Elementarsatz falsch; so besteht der Sachverhalt nicht. [TLP 4.25]

Die Gesamtheit der bestehenden Sachverhalte ist die Welt. [TLP 2.04]

Ist alles über alle Sachverhalte gesagt, dann ist auch alles über die Welt gesagt. Alle wahren Elementarsätze sagen alles über alle bestehenden und die Negationen aller falschen Elementarsätze alles über die nicht bestehenden Sachverhalte.

„Ziggy ist schwarz.“ ist kein Elementarsatz. Denn er könnte bei der selben Konstellation der Sachverhalte je nach Festlegung wahr oder falsch sein. Demnach sollten die Elementarsätze nicht von zebrigen Dingen sprechen. Das ist der Fall, denn Sachverhalte sind in Wittgensteins Theorie Verbindungen von Gegenständen [TLP 2.01] und über Gegenstände schreibt er:

Der Gegenstand ist einfach. [TLP 2.02]

Gegenstände im Sinne Wittgensteins sind folglich nicht zebrig. Sonst hätten sie verschiedene Teile und wären aus diesen zusammengesetzt. Zebrige Dinge würde er „Komplexe“ nennen. „Ziggy ist schwarz.“ ist also auch deswegen kein Elementarsatz, weil Ziggy kein Gegenstand, sondern ein Komplex ist. Propositionale Beschreibungen von Komplexen, so Wittgenstein, lassen sich aber immer in Elementarsätze zerlegen. Damit entgeht er tatsächlich dem Zebraproblem. Denn komplizierte Dinge wie Zebras, Bäume, Planeten und am Ende die ganze Welt werden beschrieben, indem man ihre nichtzebrigen Teile beschreibt.

Dazu muss er zwei Annahmen machen. Erstens, dass die ganze Welt restlos in nichtzebrige Dinge zerlegt werden kann. Zweitens, dass die zebrigen Dinge ohne Informationsverlust durch die Beschreibung ihre kleinsten nicht zebrigen Bestandteile ebenfalls beschrieben sind. Atomismus und Reduktionismus sind die passenden Ismen.

Beide Annahmen sind keine These über die Sprache, sondern über die Welt. Wittgenstein scheint folgende Überlegung zu leiten: Die Sprache, die die Welt beschreibt, ist ein Teil von ihr. Dadurch ähnelt sie ihr. Ohne diese Ähnlichkeit könnte die Sprache nichts in der Welt bezeichnen. Da die Sprache aus Elementarsätzen aufgebaut ist, muss die Welt folglich aus etwas den Elementarsätzen korrespondierendem – nämlich Sachverhalten – aufgebaut sein. Aus der Form der Sprache entnimmt er also Erkenntnis über die Form der Welt. Dem kann zweierlei entgegenhalten.

Erstens ist Sprache nicht zwingend ein Teil der Welt über die sie spricht, auch wenn dies Quine [Quine 2003] ebenso wie Wittgenstein behauptet. Z.B. wurde in Der Herr der Ringe von Tolkien auf Englisch eine Welt beschrieben, in der es kein Englisch gibt. Die Sprache ist nicht Teil der Welt, die sie beschreibt, sondern der Welt, in der wir leben. Sie kommt nur zufällig in der Welt vor über die bisweilen gesprochen wird, weil wir dort vorkommen. Die Sprache ist nicht direkt an eine Welt geheftet, sondern an uns, weil es unsere Sprache ist. Die Sprache ist nicht dort, worüber, sondern dort, wo geredet wird.

Zweitens muss die Sprache nicht unbedingt den Atomismus mit der Welt gemeinsam haben. Der Aufbau von Idealsprachen mit Elementarsätzen oder atomaren Sätzen und Pixeln hat nichts mit der Beschaffenheit der Welt zu tun, sondern ist unserer beschränkten Fähigkeiten zu lesen und schreiben geschuldet. Die Sprache muss so beschaffen sein, dass wir sie sprechen und schreiben bzw. hören und lesen können. Was für den weißen Mann der Ruf eines Käuzchens ist, ist für die Indianer das Signal zum Angriff. Ein Stamm taubstummer Indianer täte jedoch dumm daran, den Käuzchenruf zum Angriffssignal zu bestimmen, weil er dieses Signal weder geben noch wahrnehmen könnte. Menschen und ihre Maschinen sind endlich und können nur endlich viele Wörter mit je endlich vielen Buchstaben in ihrem Leben lesen oder schreiben. Wörter, die z.B. zwischen je zwei Buchstaben einen dritten enthalten, wären für uns unleserlich, unschreibbar und deswegen unbrauchbar, so wie der Käuzchenruf es für taubstumme Indianer ist.

Die Aneinanderreihung von endlich langen Zeichenfolgen zwingt zu einfachsten Zeichen, deren Teile selbst keine Zeichen mehr sind. Folglich enthält jede für den Menschen les- und schreibbare Sprache nur abzählbar unendlich viele verschiedene Ausdrücke. Um jeden Unterschied zwischen Dingen in der Welt festhalten zu können und jede Information über die Welt zu erfassen, bedarf es aber ebenso vieler verschiedener Zeichen wie Dinge in der Welt. Im besten Fall ist kein Ausdruck der Sprache leer, sondern die Beschreibung eines Dings in der Welt, die wir bewohnen. Wenn diese Welt nur abzählbar unendlich viele Dinge enthielte, wäre eine vollständige Beschreibung zwar für keinen Menschen machbar, aber zumindest mit seiner Sprache denkbar. Umfasst unsere Welt dagegen mehr Dinge, dann ist eine Beschreibung der Welt mit menschlichen Sprachen weder mach- noch denkbar. Eine vollständige Beschreibung ist also nicht eigentlich eine, bei der es nichts mehr über die Welt zu sagen gäbe, sondern eine, bei der unser Vorrat an Zeichen ausgeschöpft ist.

Man könnte Wittgenstein ein anthropomorphistisches Weltbild nachsagen. Der Elementarsatzaufbau der logischen Sprachen ist der Verfassung des Menschen und heute auch seiner Maschinen geschuldet. Er behauptet, die Welt hat sich auf strukturell gleiche Weise für den Menschen zurecht gemacht.

Die Speicher der Computer, denen sich die bereits erwähnten Mikro- und Teleskopiker bedienen, sind sämtlich endlich groß und Rechner sind auch endlich. Die Bremermann-Grenze zeigt das Ausmaß dieser Endlichkeit. [Bremermann 1967] Deswegen unterliegen die maschinenlesbaren Sprachen denselben Beschränkungen. Jede tatsächlich ausgeführte Beschreibung hat endlich viele Sätze oder Pixel. Demnach steht jeder brauchbare Beschreibung einer Mannigfaltigkeit gegenüber, die größer als ihre eigene ist. Dadurch ist jede Beschreibung gezwungen, entweder viele Dinge gar nicht zu beschreiben. Oder aber sie fasst viele Dinge zu einem zusammen und beschreibt sie als zebrigen Komplex en bloc. Eine exakte Beschreibung der Welt, in der wir leben, ist also weder mit unseren Mitteln noch mit Hilfe von Maschinen nicht möglich.

Könnte man die Mittel ändern und das TND-Kriterium beseitigen? „Ziggy ist schwarz“ wäre dann entweder weder wahr noch falsch, oder gleich beides. Es ist ziemlich egal, was von beidem wir zulassen. In einer Pixelgrafik muss das Pixel, um einen dieser Fälle anzuzeigen, eine Signalfarbe erhalten. Wir hätten also schwarz, weiße und einige Signalpixel. Wäre Rot diese Signalfarbe, würden alle unsere Digitalkameras, seien sie in Mikroskopen, Teleskopen oder nur im Urlaubsgepäck, nur noch rote Bilder machen, denn alles, was diese Geräte aufnehmen, ist zebrig. Zudem müsste die Kamera, um ein Pixel als Abbild eines zebrigen Dings zu markieren, feststellen, dass es zebrig ist. Der Sensor dieser Kamera müsste deswegen für jedes Pixel des Bildes zwei Sensorelemente haben. Messen beide Verschiedenes, dann liegt Zebrigkeit vor. Damit hat das Bild maximal die halbe Auflösung des Sensors und ist unnötig grob.

Dass wir in der Lage sind, trotz des Zebraproblems einem Zebra sehr ähnliche Bilder zu erzeugen, zeigt, dass das Zebraproblem nicht das Ende der Wissenschaft ist. Wir brauchen eine Strategie zum Umgang mit dem Zebraproblem. Die Wissenschaftler, die Maschinen in der Forschung anwenden, werden diese Strategien oftmals richtig anwenden, jedoch ohne Sie und die Fehlerquellen vollständig und allgemein zu kennen. Hier ist weiterer Forschungsbedarf.

Refbacks

• There are currently no refbacks.