From the WAB archives: A selection from the Bergen Wittgenstein archives' Working Papers and audio-visual materials

Criterion and symptom

The concept of criteria developed gradually throughout Wittgenstein's middle and later periods. For the purposes of this paper I am concerned only to give one reading of the term. Criteria function normatively and are part of the grammatical rules of application for a term. These rules are part of our form of representation. Confusions between criteria and symptoms arise when the form of representation is applicable and supportive of one grammatical proposition, but not supportive of another which appears to have the same structure. For example, first-person assertions of sensations such as "I am in pain" are regarded by Wittgenstein as a symptom of pain for the utterer, because of the lack of criteria. The private language argument discusses why there can be no criteria in this case. On the other hand, third-person assertions such as "she is in pain" which are made on the basis of observing pain behaviour, are regarded as one of many criteria of her pain for us. Another criterion would be her avowal "I am in pain".

The first-person statement is an avowal with no means of sharing the accompanying sensation. We therefore have no way of ascertaining the sincerity of the utterer and thereby the truthfulness of the avowal. Furthermore, it would be nonsense to assert "I thought I was in pain but I was mistaken" because the person making the avowal does not have [Cartesian] privileged access to data which would ensure the consistent application of the term. The avowal cannot therefore be a criterion for the utterer of whether she has a pain. In the case of the third-person assertion, we take it as one criterion of pain that certain behaviour determine the conditions under which we can appropriately say "she is in pain". Manifest behaviour accompanied by first-person avowals are usually our main criteria of third-person pain. Thus there is an unexpected asymmetry between the expressions "I am in pain" and "she is in pain" (PI-I §§246-265).

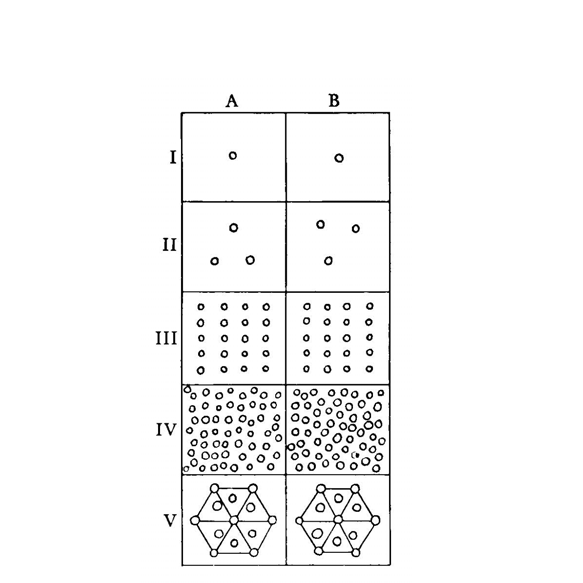
Nor does "verifiability" offer a simple substitute for the meaning of a proposition. Meaning is determined by the use of the proposition in a framework of application (PI-I §353). Thus the meaning of "sameness of number" is not determined by a single act of verifying (counting), but has several context-dependent criteria:

in I and II the number that one immediately recognizes; in III the criterion of correlation; in IV we have to count both groups; in V we recognize the same pattern. (PG p.354 Δ1258)¹

Calculation and proof

The term "calculation" is applied by Wittgenstein to non-mathematical concepts, but for the moment I will assume reference to a mathematical calculation. Calculation is a particular operation in which we draw correct inferences. Thus when we say 25x25=625 we calculate with numbers and when we say 25x25=605 we do not calculate (RFM-VI §23). When we calculate we do not "discover" something. "A calculation is not an experiment" (PI-II p.218). It is a criterion of calculation that we should accept the outcome as a correct inference. What we take as a correct inference cannot therefore be determined by calculation but by the nature of our numerical practice. This appears to leave our numerical practice open to considerable arbitrariness based on eccentricities of implementation. However, the coherence of our numerical system contributes to our notion of correct inference. Thus we can and do say (24x25)+(1x25)≡25x25.

Our use of conventions is not arbitrary but discretionary, because the fabric of our conventions is a closely woven one in which we subscribe to many conventions when we subscribe to one. However, at the outset it may be discretionary whether one convention or another is applied. What is discretionary is the sense in which one convention or form of representation may be exchanged for another while remaining useful. Utility is probably a matter of compatibility. The less exchange there is between systems the fewer are the constraints over the form of representation.

What Wittgenstein attacks is the feeling that our grammar is answerable to reality. 7+5 is an "alternative description" of 12 (Baker & Hacker p.321). 7+5=12 flows from the meaning of these signs. In another system, 7+5 might equal 13 but then 12 and 13 would mean something different, i.e. "12=13".

Correct inference is a criterion by which we test whether calculation has occurred. Likewise proof, being related to calculation with numbers, or in geometrical proof, is a certain kind of operation which needs some context of practice:

in the system α is it possible to trisect a line? What kind of trisection is meant in this question… trisection by trial and error and measurement? In that case the answer is perhaps yes. (PG-II §27 Δ1261)

In addition we are given the graphical concept that "a proof is a single pattern" (Remarks on the Foundations of Mathematics [RFM]-I §28) and "the proof serves as a picture of the experiment" (RFM-I §36).

A rectangle can be made of two parallelograms and two triangles. Proof: (RFM-I §50 Δ1045)

That we take something as a proof is a grammatical move in our game of calculating with numbers or in geometry. This brings us to our third pair of words: explain and describe.

Explanation and description

Contrary to our naive expectations, when we think we are explaining by means of the assertion of criteria, we are most commonly simply describing what constitutes our practice. We take a particular move in our language game as a proper application. Our naive expectation of the difference between description and explanation is illustrated at the beginning of PI by the Augustinian picture of language learning. The target is not whether we do in fact learn language by this means, i.e. that we learn words which are names of objects defined by ostension and that operators are learned in the context of speaking and action. What is in question is that we commonly have a view that explaining how language is acquired could be constituted by an account of this kind. On the contrary, Wittgenstein asserts (PI-I §30) that this simply describes our practice of responding to the question "how is language learned?" One move in our response-game is description by ostension. In the case of naming we take it as a criterion of correct learning that an appropriate action is performed by the learner in response to the gesture of ostension by the teacher. This is "having learned the meaning of a word".

Paradigms and graphics

the picture of a black and white patch serve us simultaneously as a paradigm of what we understand by "lighter" and "darker" and as a paradigm for "white" and "black". (RFM-I §105 Δ1055)

So what part do graphics play in this social construct? In particular, given the considerable number of graphics, are they illustrations which reveal our common misconception of an explanation as a description, or a criterion as a symptom?

In response I shall introduce a seventh term from the title of this paper and already mentioned above: paradigm. I shall use the term in the following way: that a paradigmatic word or graphic shall (a) have a certain quality so that when we compare it with something it is to that quality that we attend, and (b) that this word or graphic has a role as part of an accepted practice of reference. Let me give an example: we might take the colour of the British pillar-box as a paradigm of "red".

The pillar-box is normally red, and so meets criterion (a) by virtue of its colour. It may be that in some place a pillar-box has been painted a different colour and so although standardised it must be accepted that the "redness" and not the "pillar-box form" is the quality to which we draw attention. Of course, Wittgenstein discusses at some length the object of reference in ostensive definition, i.e. whether we can draw attention to the colour and not to the form with any reliability (PI-I §§28 & 29). He also discusses the difficulty of canonical samples, i.e. in the example above we use the pillar-box both as definiens and definiendum (PI-I §50).

Criterion (b) requires that although the pillar-box has the colour red it does not become a paradigm of red until we use it as a definiens. There are, for example, British Standard colours which must have corresponding samples locked away in a light-proof safe. Whether or not a colour is "British Standard X-XXX [pillar-box red]" depends on reference to the canonical sample rather than a particular sample in the street. Thus a sample gains the status of a paradigm in part by its use in a particular language game. If we changed the game and held that "red" was defined as the colour of the pillar-box rather than the sample, we might throw away the colour sample in the safe rather than repaint pillar-boxes.

This description of paradigms places them in a close relationship to canonical samples (PI-§50). In each case the sample provides a referent for a definition, e.g. the standard metre is the length of the so-called "standard metre" in Paris. Thus if we ask whether something is one metre in length we can/should compare it with the sample in Paris. In such systems we must be confident that the canonical sample is invariable. More particularly, it becomes meaningless to ask in this case whether the canonical sample itself has a length of one metre.

The use is similar in the case of paradigms. The paradigm has a role as a clear demonstrator of a particular quality. It is not definitive like the canonical sample, e.g. we can have a paradigm of red, being somewhere in the middle of the range of hue and saturation to which we normally apply this colour-word; whereas the canonical sample is more specific, e.g. that this red sample is BSX-XXX. But herein lies the utility of the paradigm. It may be used to demonstrate qualities which cannot have definitive [canonical] samples. "This is one metre in length" is a move in grammar equivalent to saying "I will take this as a unit of measurement called one metre". It is a definition. However, "this is a paradigm of red" is part of a social transaction about broad concept-frameworks for which a canonical sample cannot be available.

Paradigms fulfil some of the requirements of criteria but with this important supplement. We use a paradigm as an exemplar but not as a definition. This introduces a certain generality that is a feature of concepts like "red" but not of the concept "one metre in length". The philosophical, rather than commonplace, problem of generality finds expression in "the problem of the heap" (PG-I appendix 8) and in everyday concepts such as "noticeably longer" (PG-I appendix 8, Δ1183). This only becomes a philosophical problem when we seek specific boundaries to the transition from quantity a to quantity b.

In RFM-I, which is a re-ordering of the second part of an early version of PI, Wittgenstein discusses a paradigm of counting and calculating up to five in the form of "bracket notation" (RFM-I §67 Δ1049):

This shows what we mean by addition. If we have this paradigm or model then we are able to correctly infer that 3+2=5. We can also represent the commutativity of arithmetical operations, e.g. 27+16=43, 43-16=27, etc., and other internal relations by showing the sum divided by a line which may be placed anywhere along our total number (the representation in RFM-III §11 is less clear than the corresponding entry in an unpublished manuscript MS 122 p.28r reproduced here):

Commutation also applies to our understanding of spatial objects which fit together, e.g. RFM-I §70 (Δ1050):

So it is not the case that
number-concepts are defined by graphics but that these examples show the fundamentally graphical/practical foundations of our mathematical concept-framework. They show what we mean by correct inference, which is in turn bound up with our concept of the continuity of physical objects.

This is how our children learn sums; for one makes them put down three beans and then another three beans and then count what is there. If the result at one time were 5, at another 7... then the first thing we said would be that beans were no good for teaching sums. (RFM-I §37)

This comparison with practice is reinforced by Wittgenstein's thought-experiment of the tribe who calculate the price of a heap of wood by the area covered by the heap rather than the volume of wood (RFM-I §149). In other words they ignore the height. We would say they do not calculate consistently, but our concept of accuracy is bound up with our concept of three-dimensionality and value according to quantity. However, we do not always apply such a framework of calculation to monetary value. For example, we often calculate salaries not on the basis of quantity of work done (e.g. wood stacked), but on the basis of hours consumed or the age or sex of the worker.

Appropriately chosen paradigms give us the opportunity of seeing connections, of having perspicuous representations of our concepts. Seeing connections is fundamental (PI-I §122). Unfortunately only one graphical example of perspicuous representation is given, the colour octahedron (Philosophical Remarks p.278 Δ1121). Even this is described merely as adequate (genügt) rather than perspicuous (übersichtlich):

To what extent can you say that grey is a mixture of black and white in the same sense as orange is a mixture of red and yellow? And doesn't lie between black and white in the sense in which red lies between blue-red and orange? If we represent the colours by means of a double-cone, instead of an octahedron, there is only one between on the colour-circle, and red appears on it between blue-red and orange in the same sense as that in which blue-red lies between blue and red. And if in fact that is all there is to be said, then a representation by means of a double-cone is adequate, or at least one using a double eight-sided pyramid is.

The colour octahedron is thus a representation of the grammar of our colour concepts. It represents our concept-grammar, rather than being a phenomenalistic representation of colour. The octahedron links our uses of colour concepts and words. It relates what we say, e.g. white is lighter than black, to the phenomena. Other colour systems show other colour-concept relationships, e.g. that yellow is brighter than green, which the octahedron does not. In particular the octahedron shows relationships between four primary colours which are no longer fundamental to our colour concepts because of the influence of RGB or CMY colour theory. We might use this to "prove" why "there is a geometrical gap, not a physical gap, between red and green" (Zettel §354).

So why are graphics used so intensively in Wittgenstein's texts? Given the generality of the paradigm: that it is a particularly apposite example but not itself a criterion, it allows us to see beyond the ostensive definition provided by the sample, to the broader way in which this might act as a model for further applications, e.g. of the meaning of a word. It is the very ambiguity of the duck-rabbit that perspicuously illustrates aspect-blindness (PI-II p.194). In addition, graphics can be made to misrepresent a concept, e.g. Wittgenstein draws a broken square which nearly describes something, or blurs the boundaries (The Brown Book p.164), and the incremental transformation of a square into a triangle (Last Writings on the Philosophy of Psychology I §71 Δ1455-58). We have our attention drawn to the point at which the integrity of the single concept breaks down:

Conclusions

My main conclusion is to criticise Baker & Hacker's remarks on the function of the graphics. If (p.5):

inferring or drawing a conclusion is not a mental process or act, but a transformation of expressions according to paradigms. It is not answerable to something external but is a movement within grammar.

then I disagree with their description of the passive [illustrative] role of the graphics:

[Wittgenstein's] points are illustrated with very elementary examples, e.g. 25x25=625, or simple diagrammatic proofs of equations.

I propose that they are not serving [passively] as illustrations, but [actively] as the bedrock, i.e. they function normatively. Baker & Hacker go on to assert that (p.6):

we construe mathematical proofs as demonstrations of propositions from other propositions, but this too is unessential since a proof may consist of a diagram or geometrical construction to which the concepts of premises, conclusions and inference are inapplicable.

I think this is also wrong, except to the extent that we might say these words have a function only in relation to mathematics and number concepts. In the interpretation of a diagram one needs equivalent constructs. We can find in the straightness of the line, in the use of a ruler and a compass, that we have a grammar of diagrammatic construction. "A proof established internal relations" (Baker & Hacker p.8), but these can only be represented graphically by the use of certain drawing techniques and the use of instruments which themselves represent a move in [geometrical] grammar. We thereby demonstrate what we accept as correct inferences.

There is a core to Wittgenstein's project to show us our central normative concepts, not only in mathematics but in language use in general. What is normative is bound up with our form of representation (Ambrose p.16). The discretionary nature of this form of representation extends even to mathematics, where what we take as discovery through calculation is normative description (RFM-VII §6). Finally, we encounter linguistic normativity, for example when we feel the "hardness of the logical must" (PI-I §437, Baker & Hacker p.269). To this list of forms of representation which are linked by compatible norms I propose to add some graphical paradigms. The ones cited are not the only cases, c.f. RFM-I §22-69, PG-IV §18, etc.

Recapitulation

Graphics are normative in that they establish the underlying grammatical structure of concepts such as proof. They do not merely illustrate such concepts. It is the rules of graphical combination that make perspicuous what is normative within language. The paradigmatic function of graphics is related to Wittgenstein's interest in the important role of generality and prototype (ungefähr and Urbild) in conceptualisation.

This reinforces the importance of the correct representation of Wittgenstein's graphics, all of which are under revision at present. Graphics are able to show us the fine incremental slippage between what we would accept and what we would not. The boundaries are loose, with graphics functioning as paradigms rather than samples. They contribute to the therapeutic function of philosophy. The moment at which words acquire fixed boundaries is the moment at which "language goes on holiday" (PI-I §38).