Previous part
-
118

-
Ende August 36
Philosophische Untersuchungen.
Versuch einer Umarbeitung.
-

-
Augustinus beschreibt das Lernen der menschlichen Sprache so:1 (Confessiones I.8)
„... cum ... appellabant rem aliquam et cum secundum eam vocem corpus ad aliquid movebant, videbam et tenebam hoc ab eis vocari rem illam, quod sonabant, cum eam vellent ostendere”.
1 [Das Lernen der menschlichen Sprache beschreibt Augustinus so:| Augustinus beschreibt das Lernen der menschlichen Sprache so:]
-

-
Wer es1 so beschreibt, denkt vorerst an eine gewisse Klasse von Wörtern, wie etwa ‚Mann’, ‚Brot’, ‚Tisch’, und nur entfernt2 an Wörter, wie ‚nicht’, ‚aber’, ‚vielleicht’, ‚heute’.
1 [das Lernen der Sprache| es]
2 [erst in zweiter Linie| nur entfernt]
-

-
Wer das Schachspiel beschreiben wollte, aber in seiner Beschreibung die Bauern und ihre Funktion im Spiel nicht erwähnte, von dem könnte man sagen1, er habe das Schachspiel unvollständig beschrieben; aber auch: er habe ein einfacheres Spiel als unser Schach beschrieben. Und so2 kann man sagen Augustins Beschreibung gelte für eine einfachere Sprache als die unsere. – So eine einfache Sprache wäre die:3
Ihre Funktion ist die Verständigung eines Meisters A mit seinem Gehilfen B. A errichtet einen Bau, B reicht ihm Bausteine zu. Es gibt Würfel, Platten, Balken, Säulen. A ruft eines der Wörter ‚Würfel’, ‚Platte’ etc. aus, B bringt ihm darauf den Baustein4. – Denken wir uns eine Gesellschaft die nur dieses System der Verständigung, nur diese Sprache, besitzt. Die Kinder lernen die Sprache, indem sie zu ihrem Gebrauche erzogen werden: d.h., sie werden dazu erzogen, zu bauen, sich der Rufe ‚Platte!’, ‚Würfel!’, etc. zu bedienen und auf diese Rufe richtig zu reagieren. Dieses Lernen der Sprache ist wesentlich eine Abrichtung – durch Vormachen, Ermunterung, Nachhilfe, Belohnung, Strafe, u.a.m.5. Ein Teil der Abrichtung besteht etwa darin, der Lehrende weist auf einen Baustein, lenkt die Aufmerksamkeit des Kindes auf ihn, und spricht dabei ein Wort aus. Diesen Vorgang6 will ich ‚ zeigendes7 Lehren der Wörter’ nennen.
1 [Wenn jemand das Schachspiel beschreiben wollte, aber [seine Beschreibung vergäße die Bauern und ihre Züge| in seiner Beschreibung [die Bauern| die Bauern und ihre Funktion im Spiel] [unerwähnt ließe| nicht erwähnte]], so könnte man sagen| Wer das Schachspiel beschreiben wollte, aber in seiner Beschreibung die Bauern und ihre Funktion im Spiel nicht erwähnte, von dem könnte man sagen]
2 [in diesem Sinne| so]
3 [Denken wir uns die folgende Sprache:| So eine einfache Sprache wäre die:]
4 [Stein| Baustein]
5 [u.s.w.| u.a.m.]
6 [ Dies| Diesen Vorgang]
7 [vorzeigendes| zeigendes]
-
119

-
Im praktischen Gebrauch dieser Sprache ruft der Eine die Wörter als Befehle, der Andre handelt nach ihnen. Im Lernen der Sprache aber wird sich diese Übung1 finden: das Kind ‚benennt’ die Gegenstände. D.h., es sagt die Wörter, wenn der Lehrende auf die verschiedenen Bausteinformen weist. Ja es wird hier die noch einfachere Übung geben: Das Kind spricht Worte nach, die der Lehrer ihm vorsagt.
1 [dieser Vorgang| diese Übung]
-

-
„Aber in dieser Sprache hat doch das Wort ‚Platte’, z.B., nicht die selbe Bedeutung, wie in unserer Sprache!” – Das ist wahr, wenn Du sagen willst, daß in unserer Sprache das Wort ‚Platte’ auch anders verwendet wird als in (1). Aber gebrauchen wir es nicht auch ebenso wie in (1)? Oder sollen wir sagen, wenn wir es brauchen, dann ist es ein elliptischer Satz,1 eine Abkürzung für „Bring mir eine Platte”? – Ist es so: Wenn wir ‚Platte!’ rufen, so meinen wir ‚Bring mir eine Platte!’? Aber warum soll ich hier wenn ich angeben will was er meint den Ausdruck ‚Platte!’ in ‚Bring mir eine Platte!’ übersetzen, und wenn sie gleichbedeutend sind, warum soll ich nicht sagen: „Wenn wir ‚Platte!’ rufen, so meinen wir ‚Platte!’”? Oder: Warum sollte ich nicht ‚Platte!’ meinen können, wenn ich im Stande bin ‚Bring mir eine Platte!’ zu meinen? Es sei denn, daß Du sagen willst, daß ein Mensch tatsächlich, wenn er ‚Platte!’ ruft, zu sich selbst, im Geiste, immer den Satz ‚Bring mir eine Platte’ sagt. Haben wir aber einen Grund2, dies zu glauben3?
1 [, es sei dann ein elliptischer Satz,|, wenn wir es brauchen, dann ist es ein elliptischer Satz,]
2 [Ist aber ein Grund vorhanden| Haben wir aber einen Grund]
3 [anzunehmen| zu glauben]
-
120

-
Denken wir uns folgende Fragestellung: „Wenn jemand den Befehl gibt ‚Bring mir eine Platte!’, muß er ihn als Satz von vier Wörtern1 meinen; kann er ihn nicht auch als ein (langes, zusammengesetztes) Wort meinen, dem einen Worte ‚Platte!’ entsprechend?”2 – Wir werden geneigt sein, zu antworten, daß er die vier Wörter meint, wenn er ‚Bring mir eine Platte!’ im Gegensatz zu andern Sätzen gebraucht3, welche diese Wörter in andern Zusammenstellungen enthalten; wie etwa ‚Bring mir 2 Platten!’, ‚Bring ihm einen Würfel!’, etc.etc. – Aber was heißt es, den einen Befehl im Gegensatz zu diesen andern gebrauchen? Müssen dem der den einen Befehl gibt, die andern im Geiste vorschweben? Und alle von ihnen;4 oder nur einige? Ist es nicht so: Der Befehl ist ein Satz aus vier Wörtern – oder, der Befehlende ‚meint vier Wörter’ – wenn in der Sprache, die er spricht, und deren ein Satz der5 Befehl ist, jene andern Kombinationen vorkommen? Es kommt nicht darauf an, daß solche Kombinationen dem Befehlenden vorschweben, während er den Befehl gibt, noch offenbar darauf, wie lange vorher oder nachher er etwa an sie gedacht hat.
1 [vier Wörter| Satz von vier Wörtern]
2 [das dem einen Wort ‚Platte!’ entspricht?”| dem einen Worte ‚Platte!’ entsprechend?”]
3 [braucht| gebraucht]
4 [,|;]
5 [dieser| der]
-

-
Betrachten wir nun eine Erweiterung der Sprache (1). Der Gehilfe kann die Zahlwörter von ‚eins’ bis ‚zehn’ der Reihe nach hersagen. Auf den Ruf ‚Fünf Platten!’ geht er dorthin, wo die Platten aufgestapelt sind1, sagt die Zahlwörter von ‚eins’ bis ‚fünf’, nimmt bei jedem Wort eine Platte auf und bringt sie A2. (In der Praxis3 dieser Sprache sprechen beide Teile.) Zum Lernen der Sprache gehört hier4 das Auswendiglernen der Zahlwörterreihe. Der Gebrauch dieser Wörter5 wird wieder vorzeigend gelehrt; aber hier wird das gleiche Zahlwort, z.B.6 ‚drei’, sowohl beim Hinweisen auf Platten als auf Würfel u.s.w. vorgesprochen, und verschiedene7 Zahlwörter beim Hinweisen auf Steine der gleichen Form.
1 [liegen| sind]
2 [dem Bauenden| A]
3 [Im Gebrauch |In der Praxis]
4 [Das Lernen der Sprache enthält nun| Zum Lernen der Sprache gehört hier]
5 [der Zahlwörter| dieser Wörter]
6 [etwa| z.B.]
7 [und die verschiedenen| und verschiedene]
-
121

-
Dem Auswendiglernen der Zahlwörterreihe entspricht kein Zug1 im Lernen der Sprache (1), und dies zeigt klar2, daß wir mit den Zahlwörtern eine ganz neue Art von3 Instrument in die Sprache eingeführt haben. Die Wesensverschiedenheit der Instrumente Zahlwort und Bezeichnung der Bausteinform ist hier so augenfällig4, weil wir es nur mit zwei Wortarten zu tun haben und die Art des Gebrauchs der beiden5 ganz übersehen können. Die beiden Sprachinstrumente haben nur die äußere Form, die Form der Lautreihe, miteinander gemein6. Und die ist unwesentlich, denn wir könnten uns eine Variante von (2) denken,
in der A statt Zahlwörter auszusprechen, eine Anzahl von Fingern in die Höhe hebt.7
Was hat das vorweisende Lehren der Wörter ‚Platte’, ‚Würfel’, etc. mit dem der Zahlwörter gemein? In beiden Fällen weisen wir auf Dinge und sprechen Wörter aus; aber der weitere Gebrauch, den wir von dieser Handlung machen ist jedesmal ein andrer. Dies ist freilich nur offensichtlich, wenn wir Beispiele betrachten, die wir bis in ihre Einzelheiten ausgeführt haben. Man kann den Unterschied durch die Ausdrucksweise verwischen:8 „Im einen Fall weisen wir auf die Form, im andern auf die Anzahl”.
1 [nichts| kein Zug]
2 [deutlich| klar]
3 [ein gänzlich neues| eine ganz neue Art von]
4 [tritt hier so klar zutage| ist hier so augenfällig]
5 [und [ihren Gebrauch| den Gebrauch der beiden]| und die Art ihres Gebrauches| und die Art des Gebrauchs der beiden]
6 [Es ist hier klar, daß die Wortarten nur die äußere Form der Lautreihe miteinander gemein haben| Die beiden Sprachinstrumente haben nur die äußere Form, die Form der Lautreihe, miteinander gemein]
7 [ Zahlwörter auszusprechen dem B eine Anzahl von Fingern zeigt.| Zahlwörter auszusprechen, eine Anzahl von Fingern in die Höhe hebt.]
8 [Jener Unterschied wird verschleiert durch die Ausdrucksweise:| Man kann den Unterschied durch die Ausdrucksweise verwischen:]
-

122
-
Führen wir ein weiteres Werkzeug in unsere Sprache ein: Bestimmten Gegenständen, einzelnen bestimmten Steinen die beim Bau verwendet werden sollen, werden Namen (Eigennamen) gegeben, man zeigt auf den Stein und sagt seinen Namen. Ruft A den Namen aus, so bringt B den Stein, dem er beigelegt wurde.
-

-
Das vorzeigende Lehren der Worte ist hier wieder verschieden von dem in (1) und (2). Aber nicht notwendigerweise die hinweisende Gebärde, oder das Aussprechen des Eigennamens, noch, was beim Zeigen und Aussprechen im Sprechenden oder Hörenden vorgeht; wohl aber der Gebrauch der von diesem Zeigen und Aussprechen im Lehren der Sprache und in der Praxis der Verständigung mit ihr gemacht wird. – Soll man sagen, der Unterschied liege darin, daß man in den verschiedenen Fällen auf verschiedene Arten von Gegenständen weist? Aber wenn ich mit der Hand auf ein Stück weißes Papier zeige, wie unterscheidet sich ein Hinweisen auf die Form von einem Hinweisen auf seine1 Farbe? Man möchte sagen: der Unterschied ist, daß wir in den beiden Fällen Verschiedenes meinen. Und Meinen sollte hier ein Gedankenvorgang2 sein, der statthat3 während wir zeigen. Besonders neigt man zu dieser Vorstellung4, wenn man sich sagt5, daß ein Mensch, der gefragt wird, ob er die Form oder die Farbe meine,6 im allgemeinen apodiktisch im einen oder im andern Sinne antworten wird7. Suchen wir aber nach zwei seelischen Vorgängen, die das Meinen der Form und das Meinen der Farbe kennzeichnen8, so finden wir nichts, wovon wir sagen könnten, es müsse alle Handlung des Zeigens der gleichen Art begleiten. Unsere Begriffe: ‚die Aufmerksamkeit auf die Form richten’, ‚die Aufmerksamkeit auf die Farbe richten’ sind nur rohe, unbestimmte Begriffe. Der Unterschied, könnte man sagen, liegt nicht einfach in dem was beim Zeigen vor sich geht, sondern vielmehr in der Umgebung dieses Zeigens, in dem, was ihm vorhergeht und dem was darauf folgt. Es gibt aber wohl charakteristische Weisen auf eine Form zu zeigen, oder auf eine Farbe, Höhe, einen Umfang, etc..
1 [die| seine]
2 [Vorgang| Gedankenvorgang]
3 [stattfindet| statthat]
4 [Idee| Auffassung| Vorstellung]
5 [bedenkt| sich sagt]
6 [auf die Form oder auf die Farbe zeige,| die Form oder die Farbe meine,]
7 [kann| wird]
8 [charakterisieren| kennzeichnen]
-

124
-
Auf den Ruf „Diese Platte!” bringt B die Platte auf die A zeigt. Auf den Ruf „Platte dorthin!” trägt er eine Platte an die Stelle auf die A weist.
-

-
Wird das Wort ‚dorthin’ zeigend1 gelehrt? Wenn der Gebrauch dieses Wortes gelehrt und eingeübt wird, wird der Lehrende die zeigende Handbewegung machen und dabei das Wort aussprechen. Aber sollen wir sagen, daß er damit einem Ort den Namen ‚dorthin’ gibt? Die zeigende Gebärde gehört ja hier in die2 Praxis der Verständigung mittels der Sprache.
1 [vorzeigend| zeigend]
2 [zur| in die]
-

-
Es ist unter Philosophen1 die Meinung aufgetaucht, daß Wörter wie ‚dort’, ‚hier’, ‚jetzt’, ‚dieses’ die eigentlichen Eigennamen sind, nicht aber2 die Wörter, die wir für gewöhnlich so nennen würden.3 Diese seien Eigennamen nur in einem ungenauen, oder angenäherten Sinn. Denke an Russells Begriff vom ‚individual’, oder an meinen von den ‚Gegenständen’ und ihren ‚Namen’ (Logisch-philosophische Abhandlung); diese Gegenstände sollten die Grundbestandteile der Wirklichkeit sein; etwas, wovon man nicht aussagen könnte, es existiere; oder existiere nicht. (Theaitetos) Welches diese Elemente der Wirklichkeit seien4, schien nicht leicht zu sagen. Ich dachte, es sei die Aufgabe weiterer ‚logischer Analyse’ sie zu finden.5 Wir haben dagegen in (4) Eigennamen eingeführt, zur Bezeichnung von Dingen, Gegenständen, im gewöhnlichen Sinne des Wortes.
1 [in der Philosophie| unter Philosophen]
2 [und nicht| nicht aber]
3 [im gewöhnlichen Leben etwa so nennen.| für gewöhnlich so nennen würden.]
4 [waren| seien]
5 [. Sie zu finden dachte ich mir als die Aufgabe weiterer ‚logischer Analyse’. |. Ich dachte, es sei die Aufgabe weiterer ‚logischer Analyse’ sie zu finden.]
-

125
-
Frage und Antwort. A fragt: „Wie viele Platten?” B zählt sie und antwortet mit dem letzten Zahlwort.
-

-
Systeme der Verständigung wie meine Beispiele 1-6 will ich ‚Sprachspiele’ nennen. Sie sind dem, was wir im gewöhnlichen Leben Spiele nennen mehr oder weniger verwandt; Kinder lernen ihre Muttersprache mittels solcher Sprachspiele, und hier haben sie vielfach den unterhaltenden Charakter des Spiels. – Wir betrachten aber die Sprachspiele nicht als die Fragmente eines Ganzen ‚der Sprache’,1 sondern als in sich geschlossene Systeme der Verständigung, als einfache, primitive, Sprachen. Um diese Betrachtungsart im Auge zu behalten ist es oft nützlich sich das Bild weiter auszumalen und sich einen primitiven Volksstamm vorzustellen dessen gesamte Sprache in diesem Sprachspiel besteht. (Denke an die primitive Arithmetik wilder2 Stämme.)
1 [einer Sprache,| eines Ganzen ‚der Sprache’,]
2 [solcher| wilder]
-
126

-
Wenn wir in der Schule spezielle technische Zeichensprachen lernen, wie den Gebrauch von Diagrammen und Tabellen, Darstellende Geometrie, chemische Formeln1, etc., lernen wir weitere Sprachspiele.
1 [Gleichungen| Formeln]
-

-
(Die Sprache des Erwachsenen stellt sich unsrem Auge dar1 als eine nebelhafte Masse, die Umgangssprache, umgeben von einzelnen, mehr oder weniger klar umrissenen, Sprachspielen, den technischen Sprachen.)
1 [erscheint uns| stellt sich unsrem Auge dar]
-

-
Fragen nach dem Namen. Es werden außer den alten Bausteinformen neue zugebracht. B zeigt dann auf eine solche Form und fragt: „Wie heißt das?” A antwortet: „Das heißt ...” Beim Bauen ruft A das neue Wort (‚Prisma’ z.B.) und B bringt den Stein.
-

-
Die Worte „Das heißt ...” mit der hinweisenden Gebärde nennen wir ‚hinweisende Erklärung’ oder1 ‚hinweisende Definition’. In (7) wird ein Gattungsname, der Name einer Form, erklärt; aber analog kann nach dem Eigennamen eines Dinges, dem Namen einer Farbe, einer Zahl, einer Himmelsrichtung gefragt werden. (Wenn wir hier von den ‚Namen’ von Farben, Zahlen, Richtungen, etc. sprechen, so könnte das zweierlei Gründe haben. Der eine: wir könnten meinen, daß die Funktionen eines Eigennamens, Farbnamens, Stoffnamens, Zahlwortes, etc., in der Sprache, d.i. ihre Funktionen im Sprachspiel, einander viel ähnlicher sind als wirklich der Fall ist. Dann sind wir versucht zu denken, die Funktion eines jeden Wortes sei ungefähr die des Eigennamens einer Person, oder etwa eines Wortes wie ‚Tisch’, ‚Sessel’, ‚Tür’. – Der andre Grund: wir verstehen die gänzliche Verschiedenheit der Funktionen des Wortes „Sessel” einerseits und eines Eigennamens andrerseits, und die Verschiedenheit beider von der, etwa, eines Farbnamens; und wir können darum auch von ‚Zahlnamen’, ‚Richtungsnamen’ etc. sprechen: Nicht, um damit zu sagen, daß Farben, Körper, Zahlen, Richtungen ja nur verschiedene Arten von Gegenständen seien, sondern um die Analogie zu betonen, die im Mangel der Ähnlichkeit liegt, zwischen den Funktionen von ‚Sessel’ und ‚Jakob’ einerseits, und ‚Süden’ und ‚Jakob’ andrerseits.
1 [,| oder]
-

127
-
B erhält eine Tabelle in welcher Schriftzeichen den Bildern von Gegenständen gegenüberstehn; z.B. den Bildern eines Hammers, einer Zange, einer Säge. A schreibt eines jener Zeichen auf eine Tafel, B sucht es in der Tabelle auf, fährt mit dem Finger vom Schriftzeichen zum Bild und holt den Gegenstand den das Bild zeigt.
-

-
Betrachten wir die verschiedenen Arten von Zeichen in unsern Beispielen. Wir wollen zwischen Sätzen und Wörtern unterscheiden. ‚Sätze’ und ‚Wörter’ in unsern Sprachspielen werde ich nennen, was dem analog ist, was wir in der gewöhnlichen Sprache ‚Sätze’ und ‚Wörter’ nennen. Ein Satz kann auch aus einem einzigen Wort bestehen. In (1) sind die Ausrufe ‚Platte!’, ‚Balken!’ solche Sätze. In (2) hat jeder Satz zwei Wörter. – Wir unterscheiden unter den Sätzen Befehle, Fragen, Behauptungen, Vermutungen, u.s.f.; unzählige Arten von deren einigen nach und nach die Rede sein soll1.
1 [wird| soll]
-

128
-
In einem Sprachspiel ähnlich (1) ruft A Befehle von der Form „Platte, Säule, Prisma!”; B bringt darauf diese Bausteine. Wir könnten hier den Befehl einen Satz, aber auch drei Sätze nennen.
-

-
– Wenn aber die Reihenfolge der Wörter dem B die Reihenfolge angibt, in welcher er die Steine bringen soll, dann werden wir „Platte, Säule, Prisma!” einen Satz nennen der aus drei Wörtern besteht1.
1 [aus drei Wörtern nennen| nennen der aus drei Wörtern besteht]
-

-
Hätte der Befehl die Form „Platte, dann Säule, dann Prisma!”, so würden wir sagen er bestehe aus vier Wörtern (nicht aus fünfen).
-

-
Unter den Wörtern finden wir Gruppen mit ähnlichen Funktionen im Sprachspiel. Man sieht leicht die Ähnlichkeit der Funktion in der Gruppe der Wörter ‚eins’, ‚zwei’, ‚drei’ etc., und anderseits in der Gruppe ‚Platte’, ‚Säule’ etc.. So unterscheiden wir Wortarten. In (9) und (10) besteht ein Satz aus Wörtern nur einer Wortart.
-

-
Die Ordnung, in der B die Steine zureicht wird durch Ordnungszahlwörter, etwa ‚erstens’, ‚zweitens’, ‚drittens’ etc., angegeben. Der Befehl in (10) kann also lauten „Drittens Prisma, erstens Platte, zweitens Säule!” Wir sehen: was in einer Sprache die Funktion von Wörtern ist, kann in einer Andern etwa von der Ordnung der Wörter geleistet werden. – Eine Pause in einem1 Satz der einen Sprache kann die Funktion eines Worts im Satz einer andern Sprache haben.
Solche Überlegungen können uns die ungeheure Mannigfaltigkeit der Mittel unserer Sprache ahnen lassen; und es ist interessant mit2 dem was sich uns hier zeigt zu vergleichen, was Logiker vom Bau aller Sätze gesagt haben. (Dies gilt auch von dem, was ich3 selbst in der Logisch-philosophischen Abhandlung geschrieben4 habe.)
1 [im| in einem]
2 [merkwürdig, mit| interessant mit]
3 [Vergleiche auch, was ich |Dies gilt auch von dem, was ich ]
4 [gesagt| geschrieben]
-
129

-
Wenn wir nach der Ähnlichkeit der Funktionen der Wörter Wortarten unterscheiden, so ist leicht zu sehen daß man verschiedenerlei Einteilungen treffen kann. Wir können z.B. leicht einen Grund finden, das Wort ‚eins’ nicht zur gleichen Art wie die Wörter ‚zwei’, ‚drei’, ‚vier’, etc. zu rechnen1.
1 [zählen| rechnen]
-

-
Denken wir uns diese Variation von1 (2): Statt „Eine Platte!”, „Einen Würfel!”, etc. ruft A einfach „Platte!”, „Würfel!”, etc.. Die andern Zahlwörter aber werden wie in (2) ausgerufen. Wer an dieses System gewöhnt wäre, würde2 das Zusammenfassen von ‚eins’ mit ‚zwei’ und ‚drei’ etc. befremdlich finden. (Denke an Gründe für und gegen die Klassifikation der ‚0’ mit den andern Kardinalzahlzeichen. – Sind Schwarz und Weiß Farben? In manchen Fällen rechnet man sie unter die Farben, in manchen nicht.)
1 [der Sprache| von]
2 [könnte| würde]
-

-
Wörter lassen sich in vielen Beziehungen mit Schachfiguren vergleichen. Denke an die verschiedenen Arten die Schachfiguren zu klassifizieren. (z.B. in Offiziere und Bauern.)
-

-
Es ist uns natürlich die hinweisenden Gebärden in (5) und die Bilder in (8) zu den Instrumenten der Sprache zu rechnen. (Es gibt Gebärdensprachen.) Die Bilder in (8) und andere Instrumente der Sprache die eine ähnliche Funktion haben will ich ‚Muster’ nennen, zum Unterschiede von ‚Wörtern’. Wenn wir von einem Muster Gebrauch machen, so vergleichen wir etwas mit dem Muster. Wir vergleichen in (8) einen Hammer mit dem Bild des Hammers, aber in (1) nicht eine Platte mit dem Wort ‚Platte’. –Wir wollen aber nicht sagen: „Es gibt in der Sprache Worte und Muster”, als wäre damit irgend ein wesentlicher Dualismus festgestellt, sondern nur einen wichtigen Gegensatz, unter vielen andern, hervorheben. ‚1’, ‚2’, ‚3’ z.B. werden wir Wörter nennen, die Zeichen ‚|’, ‚||’, ‚|||’, ‚||||’, ‚|||||’ etc. aber Muster (soweit sie nicht wieder einfach als Ziffern benützt werden). Soll man aber ‚|’ überhaupt ein Muster nennen? Es gibt Übergänge zwischen Wort und Muster. Dasselbe Zeichen könnte1 einmal als Wort, einmal als Muster fungieren2: Ein Kreis kann der Name einer Ellipse sein, aber auch das Muster, womit sie nach gewissen Projektionsregeln zu vergleichen ist.
1 [kann| könnte]
2 [gebraucht werden| fungieren]
-
130

-
Vergleiche diese beiden Zeichensysteme:
A gibt dem B Befehle die aus zwei auf eine Tafel gemalten Zeichen bestehen. Das erste Zeichen ist ein unregelmäßig geformter Fleck von irgendeiner bestimmten Farbe, z.B. grün; das zweite eine gezeichnete geometrische Figur, z.B. ein Kreis: B bringt darauf dem A einen Gegenstand, der die Farbe des ersten und die Form des zweiten Zeichens hat (z.B. einen grünen, kreisförmigen Gegenstand).
Ein Befehl ist ein gemaltes Zeichen, eine geometrische Figur in einer bestimmten Farbe gemalt, z.B. ein grüner Kreis. B bringt auf den Befehl einen Gegenstand von der Form und Farbe des Zeichens.
-
131

-
In (13) besteht ein Satz aus zwei Mustern, deren jedes einem Wort entspricht – z.B. „grüner Kreis”. In (14) dagegen steht statt dieser zwei Muster eines; das man nicht in zwei Bestandteile (Form und Farbe) zerlegen kann; es steht also hier nicht ein Muster für ein Wort.
-

-
Worte in Anführungszeichen kann man Muster nennen; in dem Satz „Er ruft ‚Halt’” also ‚Halt’ ein Muster. Vergleiche aber die beiden Fälle: der Satz „Er ruft ‚Halt’” ist ein gesprochener Satz, und anderseits ein geschriebener Satz. Wie wird das gesprochene Wort mit dem Ruf verglichen, wie das geschriebene? Wer Geschriebenes kopiert vergleicht was er schreibt mit einem Muster, aber in gewissem Sinne auch der, der nach Diktat schreibt.
Wir nennen eine große Mannigfaltigkeit von Vorgängen: „etwas mit einem Muster vergleichen”.
-

-
In (8) vergleicht B Bilder mit Gegenständen. Aber worin besteht dieses Vergleichen? Was tut der, welcher1 vergleicht? Betrachte diese Fälle: a) die abgebildeten Gegenstände sind (wie in (8)) ein Hammer, eine Zange, eine Säge, ein Bohrer; b) zwanzig verschiedene Arten von Schmetterlingen. Wie verschieden wird hier der Vorgang des Vergleichens sein? c) Die Bilder sind maßstabgerechte Zeichnungen von Bausteinen und das Vergleichen hat mit dem Zirkel zu geschehn.
1 [der| welcher]
-
132

-
Es sei B's Aufgabe ein Stück Tuch von der Farbe eines Musters zu bringen, das ihm gegeben wird. Wie vergleicht er die Farbe des Musters und des Tuches? Stelle Dir verschiedene Fälle vor:
A zeigt dem B das Muster; darauf geht B und bringt einen Stoff nach dem Gedächtnis.
B geht mit dem Muster zu dem Regal auf dem die Stoffe liegen und sieht vom Muster auf die Stoffe ehe er wählt.
B legt das Muster auf jeden der Stoffe am Regal und wählt den Stoff dessen Farbe er nicht vom Muster unterscheiden kann.
Stelle Dir dagegen den Fall vor, der Befehl lautete: „Bring mir einen Stoff etwas dunkler als dieses Muster!”. –
-

-
Ich sagte in (15) B bringe einen Stoff ‚nach dem Gedächtnis’; aber dieser Ausdruck umfaßt unzählige mögliche Vorgänge. Denke an einige Beispiele:
B, wenn er zu den Stoffen kommt, schließt die Augen und ruft sich ein Bild des Musters ins Gedächtnis. Er sieht dann abwechselnd auf die Stoffe und stellt sich das Muster vor. Einmal sagt er „zu hell”, einmal „zu dunkel”; endlich blickt er auf einen und sagt „gut!”, und nimmt ihn vom Regal.
B ruft sich kein Bild des Musters vor Augen. Er sieht einen Stoff nach dem andern an, runzelt die Stirn und schüttelt bei jedem den Kopf; beim zehnten entspannt sich sein Gesicht, er nickt mit dem Kopf und nimmt den Stoff. Denke Du hättest zu beschreiben, was Du in einem solchen Falle wirklich getan hast.
B ruft sich kein Bild des Musters vor Augen; er blickt der Reihe nach auf einige Stoffe, den fünften nimmt er und bringt ihn dem A.
-
133

-
Die Beschreibungen dieser drei Beispiele, besonders des letzten, haben etwas Unbefriedigendes. Es scheint, sie geben allerlei Nebensächliches lassen aber das Wesentliche aus. Das Wesentliche aber wäre die1 spezifische Erfahrung des Vergleichens und des Erkennens.
Wenn wir nun irgendwelche Vorgänge des Vergleichens genau ins Auge fassen, so sehen wir leicht eine Anzahl von Handlungen, Gedanken, Empfindungen, die alle für das Vergleichen mehr oder weniger charakteristisch sind. Und das ist der Fall, ob es sich um ein Vergleichen nach dem Gedächtnis handelt, oder um das Vergleichen zweier Gegenstände, die wir beide vor Augen haben. Wir kennen eine Unzahl solcher Vorgänge des Vergleichens; sie bilden, wie wir uns ausdrücken wollen, eine „Familie”. Zwischen ihren Mitgliedern besteht eine große Zahl von Ähnlichkeiten die sich auf die verschiedenste Weise übergreifen und kreuzen.2 – Wir halten Gegenstände, deren Farbe wir vergleichen wollen für kürzere oder längere Zeit zueinander, schauen sie abwechselnd an, halten sie in verschiedene Beleuchtungen, wir machen dabei verschiedene charakteristische Äußerungen, haben Erinnerungsbilder, Gefühle der Spannung und Entspannung, Befriedigung und Unbefriedigung, die verschiedenen Gefühle der Anstrengung in den Augen und ihrer Umgebung, die längeres aufmerksames Schauen begleiten und alle möglichen Kombinationen dieser und anderer Erfahrungen. Je mehr Fälle des Vergleichens und je genauer wir sie besehen, desto weniger glauben wir an eine spezifische Erfahrung des Vergleichens.
1 [eine| die]
2 [, unter deren Gliedern eine Unzahl von Familienähnlichkeiten besteht, [die einander auf die verschiedenste Weise übergreifen und kreuzen.| diese Ähnlichkeiten übergreifen und kreuzen sich auf mannigfache Weise.]|. Zwischen ihren Mitgliedern besteht eine große Zahl von Ähnlichkeiten die sich auf die verschiedenste Weise übergreifen und kreuzen.]
-
134

-
Ja, wenn Du eine Anzahl solcher Fälle genau besehen hast und ich gebe Dir nun zu, daß es vielleicht eine Erfahrung gibt, die allen von ihnen gemeinsam ist und erkläre mich bereit das Wort ‚Vergleich’ nur da zu gebrauchen, wo diese Erfahrung anwesend ist, dann wirst Du nun fühlen, daß die Annahme einer solchen Erfahrung jetzt ihren Zweck verloren hat, denn nun steht diese Erfahrung neben einer Menge anderer Erfahrungen, welche die Verbindung der Fälle des Vergleichens herstellen. – Denn jene ‚spezifische Erfahrung’, die wir suchten, sollte ja gerade das tun was nun jene Masse von Erfahrungen leistet. Die spezifische Erfahrung sollte ja nicht eine unter1 einer Anzahl mehr oder weniger charakteristischer Erfahrungen sein. – Man könnte sagen, man kann diesen Gegenstand auf zweierlei Weise ansehn: einmal aus der Nähe –, einmal von weitem und durch eine eigentümliche Atmosphäre. – Und wir haben gefunden, daß der tatsächliche Gebrauch des Wortes „Vergleich” ein anderer ist als der, den wir vom Weiten zu sehen glauben. Wir finden, daß das, was die Fälle des Vergleichens verbindet, eine große Anzahl einander übergreifender Ähnlichkeiten ist; und wenn wir dies sehen, so fühlen wir uns nicht mehr gezwungen zu sagen, es müsse allen diesen Fällen eines gemeinsam sein. Sie sind durch ein Tau mit einander verbunden; und dieses Tau verbindet sie nicht dadurch, daß2 irgend eine Faser in ihm von einem Ende zum andern läuft, sondern dadurch, daß3 eine Unzahl von Fasern einander übergreifen.
1 [aus| unter]
2 [hält nicht darum, weil| verbindet sie nicht dadurch, daß]
3 [weil| dadurch, daß]
-

-
„Aber in dem Fall (21) handelt ja B gänzlich automatisch. Wenn wirklich nur das vorgeht, was dort beschrieben ist, weiß er ja nicht, warum er den Stoff gewählt hat, er hat keinen Grund ihn zu wählen. Wenn er den richtigen wählt, so tut er es, wie eine Maschine es tun kann.” – Aber wir sagten ja nicht, daß B in diesem Falle nichts empfinde,1 daß er die Stoffe nicht sähe, keine Tast- und Muskelempfindungen habe u.s.f. – Und wie sieht denn so ein Grund aus der die Wahl zu einer nicht-automatischen macht; d.h., wie stellen wir uns ihn vor? Ich denke, wir würden sagen, daß das Gegenteil des automatischen Wählens, sozusagen das Ideal des bewußten Wählens, darin bestehe, daß wir ein klares Erinnerungsbild oder das Muster selbst vor Augen hätten und eine spezifische Empfindung nicht zwischen dem Muster und dem gewählten Stoff unterscheiden zu können. Diese bestimmte Empfindung wäre dann der Grund, die Rechtfertigung unsrer2 Wahl. Diese Empfindung, könnte man sagen, verbindet die beiden Erfahrungen: das Sehen des Musters mit dem Sehen des Stoffes. Aber was verbindet dann die spezifische Empfindung mit jenen beiden Erfahrungen? – Wir leugnen nicht, daß so eine Empfindung vermitteln kann; aber so betrachtet erscheint nun die Unterscheidung ‚automatisch – nicht automatisch’ nicht mehr so scharf und primär wir früher. Das heißt nicht, daß diese Unterscheidung in speziellen Fällen ihren praktischen Wert verliert. So werden wir unter bestimmten Umständen auf die Frage „Hast Du diesen Stoff mechanisch vom Regal genommen, oder hast Du Dir etwas dabei gedacht?” antworten, wir hätten nicht mechanisch gehandelt, denn wir hätten den Stoff genau besehen, uns an das Muster erinnert, Zweifel und Befriedigung geäußert. Das kann in einem besondern Fall der Unterschied zwischen automatisch und nicht-automatisch sein. In einem andern dagegen werden wir vielleicht zwischen automatischem und nicht-automatischem Auftreten eines3 Erinnerungsbildes unterscheiden, u.s.f..
1 [wahrnimmt,| empfinde,]
2 [der| unsrer]
3 [des| eines]
-
136

-
„Aber warum hat er in (21) gerade diesen Stoff gebracht, wie hat er ihn als den richtigen erkannt, woran?” – Wenn Du fragst „Warum?” fragst Du nach der Ursache oder nach dem Grund? Wenn nach der Ursache so ist es ja nicht schwer sich eine physiologische oder psychologische Hypothese auszudenken die die Wahl unter den gegebenen Umständen erklären könnte. Es ist die Aufgabe der experimentellen Wissenschaft solche Hypothesen zu prüfen. Wenn Du dagegen nach dem Grund fragst, so ist die Antwort: es muß kein Grund für die Wahl vorhanden gewesen sein.1 Ein Grund ist ein Schritt, der dem Schritt der Wahl vorhergeht. Aber warum sollte jedem Schritt ein anderer vorhergehen?2
1 [keinen Grund für die Wahl [geben| gegeben haben].| kein Grund für die Wahl vorhanden gewesen sein.]
2 [andrer Schritt vorangehen?| anderer vorhergehen?]
-

-
„Aber dann hat B den Stoff nicht wirklich als den richtigen erkannt.” – Wenn Du willst so brauchst Du (21) nicht unter die Fälle des ‚Erkennens’ zu zählen. Aber wenn es uns klar wird daß die Vorgänge des Erkennens eine große Familie bilden mit einander übergreifenden Familienähnlichkeiten, werden wir wahrscheinlich nicht abgeneigt sein den Fall (21) zu dieser Familie zu rechnen. – „Aber fehlt denn dem B in diesem Fall nicht das Kriterium wonach er den Stoff als den rechten erkennen kann? In (19) hatte er z.B. das Erinnerungsbild und er erkannte den Stoff durch seine Übereinstimmung mit diesem Bild.” – Aber hatte er auch ein Bild vor sich von dieser Übereinstimmung? Ein Bild mit dem er die Übereinstimmung zwischen Muster und Stoff vergleichen konnte, um zu sehen, ob es die richtige Übereinstimmung sei? Und hätte er andrerseits nicht ein solches Bild haben können? Angenommen etwa, A wollte, daß B sich erinnerte, daß hier ein Stoff von der gleichen Farbe wie das Muster verlangt sei, – im Gegensatz zu anderen Fällen etwa, in denen B einen Stoff von etwas dunklerer Farbe als das Muster bringen mußte. A gibt also1 dem B ein Muster von der gewünschten Übereinstimmung mit, nämlich zwei Stücke Stoff von gleicher Farbe. – Ist irgend ein solches Zwischenglied zwischen dem Befehl und der Ausführung notwendig das letzte? – Und wenn Du sagst, daß B in (20) wenigstens das Gefühl der Entspannung hat, woran er erkennen kann, daß der Stoff der richtige ist, – mußte er ein Bild von dieser Entspannung vor sich haben, um danach die Empfindung zu erkennen, nach der er den richtigen Stoff erkennen sollte?
1 [nun| also]
-
137

-
„Aber angenommen nun B bringt in (21) den Stoff und wenn man ihn mit dem Muster vergleicht, so erweist er sich als der unrechte.” – Aber hätte das nicht auch in den andern Fällen so geschehen können? Angenommen in (19) hätte der Stoff den B brachte nicht mit dem Muster übereingestimmt würden wir nicht in gewissen Fällen sagen, sein Erinnerungsbild habe nicht gestimmt, in andern, das Muster, oder der Stoff, habe seine Farbe geändert, und noch in anderen, die Beleuchtung sei nicht die gleiche? Es ist nicht schwer Fälle zu erfinden, sich Umstände vorzustellen, in denen man diese Urteile fällen würde. – „Aber ist nicht doch ein wesentlicher Unterschied zwischen den Fällen (19) und (21)?” – Gewiß! Eben der, welchen die Beschreibungen zeigen.
-
138

-
Im Beispiel (1) lernt B einen Baustein bringen wenn er das Wort ‚Würfel’ hört. Wir könnten uns vorstellen, daß in diesem Fall folgendes geschieht: in B ruft das Hören des Wortes ein Vorstellungsbild auf; die Erziehung, Abrichtung, hat, wie man sagen würde, diese Assoziation geschaffen. B nimmt nun den Stein auf der mit dem Vorstellungsbild übereinstimmt. – Aber mußte dies geschehen? Wenn die Abrichtung es bewirken konnte, daß das Vorstellungsbild – automatisch – B vors Auge trat, warum dann nicht daß B den Stein aufnimmt, ohne Vermittlung eines Bildes? Das bedeutet ja nur ein etwas anderes Funktionieren des Apparates der Assoziation.1 Denke daran, daß er das Vorstellungsbild nicht aus dem Wort ableitet (aber wäre es so, so würde das unser Argument nur einen Schritt zurück schieben) sondern daß der Fall hier analog dem des Registrators ist: wenn ein bestimmter Knopf gedrückt wird erscheint ein bestimmtes Täfelchen. Ja dieser Mechanismus kann statt dem der Assoziation verwendet werden.
1 [Assoziationsapparates.| Apparates der Assoziation.]
-

-
Es ist oft klärend sich das Vorstellen von Farben, Gestalten, Tönen, etc.etc., das im Gebrauche der Sprachen eine Rolle spielt ersetzt zu denken durch das Anschauen wirklicher Farbmuster, das Hören wirklicher Töne, etc., also z.B. das Aufrufen eines Erinnerungsbildes einer Farbe durch das Ansehen eines wirklichen Farbmusters, das wir bei uns tragen, viele der Vorgänge beim Gebrauch der Sprache verlieren, wenn man an die Möglichkeit dieser Ersetzung denkt, den Schein des Ungreifbaren, Okkulten.
-
139

-
Die Abrichtung im Gebrauch der Tabelle (wie der in (8)) kann dahin gehen, den Schüler nicht bloß zum Gebrauch einer bestimmten Tabelle sondern zum Gebrauch und auch zum Anlegen beliebiger Tabellen, beliebiger Kombinationen von Schriftzeichen und Bildern, zu befähigen. Die erste Tabelle die er gebrauchen lernte war etwa die in (8).
-

-
Wir fügen ihr nun das Bild eines andern Werkzeugs bei welches der Schüler vor sich hat, etwa eines Hobels, und gegenüber dem Bild das Wort ‚Hobel’. Wir werden diese Tabelle der ersten so ähnlich als möglich gestalten; auf dem gleichen Stück Papier, etwa, das Bild des Hobels unter die andern Bilder, das Wort unter die andern Wörter setzen. Der Schüler wird nun ermuntert werden, von dem neuen Bild und Wort Gebrauch zu machen ohne daß man die frühere Abrichtung an ihnen wiederholt. Das Ermuntern nun besteht in gewissen Nachhilfen, billigenden und mißbilligenden Mienen des Lehrers, Gesten, die ein Fortsetzen ausdrücken und dergleichen mehr. Denke an die verschiedenen Gebärden und Bewegungen, die man macht, um einen Hund zum Apportieren zu bringen. Aber nicht jedes Tier wird auf diese Gebärden reagieren, wie der Hund. Eine Katze wird diese Gebärden nicht, oder mißverstehen; das heißt in diesem Fall einfach: sie wird nicht apportieren. Und wenn das Kind auf unsere Ermunterungen nicht reagiert, wie eine Katze der man das Apportieren lehren möchte, so gelangt es nicht zum Verständnis einer Erklärung; oder vielmehr, das Verstehen beginnt hier mit dem Reagieren in bestimmter Weise. – Das Verstehen ermunternder Worte ist nur eine Weiterentwicklung des Reagierens auf einen ermunternden Tonfall, eine Gebärde, etc.
-
140

-
Der Schüler lernt Dingen Namen seiner eigenen Erfindung zu geben und die Dinge zu bringen, wenn die Namen gerufen werden. Es wird ihm eine Tabelle gegeben auf deren einer Seite er Bilder ihm bekannter Gegenstände findet und ihnen gegenüber, dort wo in den früheren Spielen Schriftzeichen standen, leere Stellen. Er schreibt die neuen Wörter an diese Stellen und gebraucht die Tafel dann, wie in (8).
-

-
Im1 Lernen des Gebrauchs der Tabelle kann es eine wichtige Übung sein den Finger in der Tabelle immer von links nach rechts (vom Schriftzeichen zum entsprechenden Bild) zu bewegen, gleichsam also eine Reihe paralleler Striche in ihr zu ziehen. Dies mag dann beim Übergang in (22) von der ersten Tafel zur erweiterten helfen.
1 [Beim| Im]
-

-
Tabellen und hinweisende Erklärungen und ähnliches werde ich, in Übereinstimmung mit dem gewöhnlichen Sprachgebrauch, ‚Regeln’ nennen.
-

-
Betrachte dieses Beispiel: Es werden verschiedene Arten eingeführt Tabellen zu lesen. Jede der Tabellen besteht aus zwei Kolumnen, in der einen Schriftzeichen in der andern Bilder, wie oben. Sie werden entweder horizontal von links nach rechts gelesen, wie oben, also nach dem Schema
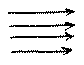
oder aber nach Schemata wie z.B.
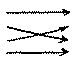
oder
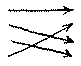 etc.
etc.
Schemata dieser Art werden den Tabellen als Regeln des Lesens beigegeben.
-
141

-
Könnten aber diese Regeln nicht durch weitere Regeln erklärt werden? – Gewiß. – Andrerseits aber: ist eine Regel unvollständig erklärt wenn ihr keine weitere Regel für ihren Gebrauch beigegeben wurde1?
1 [ist| wurde]
-

-
Wir wollen nun die endlose Reihe der Kardinalzahlen in unsre Sprachspiele einführen. Aber wie machen wir das? Die Analogie zwischen dem Spiel mit zehn Zahlwörtern und einem solchen, unbegrenzten, Spiel kann ja nicht dieselbe sein, wie die zwischen dem Spiel mit zehn und einem mit 55 Zahlwörtern. Angenommen das Spiel sei wie (2) die Reihe der Zahlzeichen aber unbegrenzt. Es werde in der Praxis des Spiels tatsächlich bis 155 gezählt, dann soll ja das unbegrenzte Spiel nicht das sein, welches aus (2) würde, wenn ich dort statt „die Zahlwörter von ‚eins’ bis ‚zehn’” „die Zahlwörter von ‚eins’ bis ‚hundertfünfundfünfzig’” gesagt hätte. Aber worin liegt dann der Unterschied? Fast möchte man so etwas sagen wie, er liege im Geiste in dem die Spiele gespielt würden.
Der Unterschied zwischen zwei Brettspielen kann z.B. in der Zahl der Spielsteine1 liegen, in der Zahl der Felder des Brettes, oder darin, daß diese2 im einen Fall Quadrate im andern Sechsecke sind, etc. Aber der Unterschied zwischen dem begrenzten und dem unbegrenzten Spiel scheint nicht in den materiellen Werkzeugen des Spiels liegen zu können, denn, möchten wir sagen, wie kann sich das Unendliche in diesen ausdrücken? Wir können es, so scheint es, nur in unsern Gedanken erfassen. Und es scheinen also die Gedanken zu sein, die das begrenzte Spiel vom unbegrenzten unterscheiden. Seltsam ist es dann nur, daß wir diese Gedanken über das Unendliche in Worten und Gebärden ausdrücken können.
1 [Spielfiguren| Spielsteine]
2 [sie| diese]
-
142

-
Denke Dir zwei Kartenspiele: Ich will sie das ‚begrenzte’ und das ‚unbegrenzte’ nennen. Die Karten beider tragen Ziffern und die höhere Ziffer sticht die geringere1. Die Spielregeln sind einander in jeder Beziehung analog; aber das eine Spiel wird mit 32 Karten gespielt das andere mit einer beliebigen Zahl. Angenommen nun wir spielen das unbegrenzte Spiel, und die Zahl der Spielkarten ist 32; wie unterscheidet sich das Spiel vom begrenzten? – Nicht durch die Blätter, nicht durch die Art wie ausgespielt, gestochen wird, etc. Aber vielleicht dadurch: Das begrenzte Spiel wird mit einem Pack gedruckter Karten gespielt, beim unbegrenzten wird jedem Spieler ein Vorrat leerer weißer Karten und ein Bleistift zum Schreiben der Ziffern gegeben; zu Anfang des unbegrenzten Spiels fragt einer: „Wie hoch gehen wir?”; und dergleichen mehr. Es wird also hier über die Grenzen des Spiels eine Entscheidung getroffen und dies kann sich in der mannigfachsten Weise abspielen. Man kann also hier wirklich sagen, was das unbegrenzte Spiel charakterisiere, sei ‚schwer zu fassen’, wenn es auch kein ungreifbarer ‚Geist’ ist. Denke endlich an die Verschiedenheit des Vorgangs der Einübung, des Lernens, der beiden Spiele. Die Partie des unbegrenzten Spiels mit 32 Karten wird sich vielleicht von einer des begrenzten Spieles kaum unterscheiden, oder nur in Dingen, die man ‚unwesentliche Äußerlichkeiten’ nennen möchte.
Der verschiedene ‚Geist’ dieser Partien mag nur darin liegen, daß sie verschiedenen Systemen angehören, und dies in den mannigfachen Beziehungen, die sie zu andern Partien und zu verschiedenen andern Vorgängen haben, die außerhalb der beiden Partien selbst liegen. Betrachte die folgenden beiden Spiele:
Es sind zwei Arten des Damespiels, ich will sie A und B nennen. In A verliert der der seine Spielsteine verliert; in B gewinnt, wer seine Steine verloren hat. Die beiden Spiele sind einander also in dieser2 Beziehung entgegengesetzt; in allen andern, nehme ich an, gleich. Welchen Unterschied wird nun ein Zuschauer sehen, der Partien der beiden Spiele A und B beobachtet? Nun, es lassen sich ja leicht solche Unterschiede beschreiben. Zuerst etwa so: In A trachtet Jeder, seine Steine davor zu bewahren, daß sie von denen des Andern übersprungen werden; in B schiebt Jeder dem Andern seine Steine zu, um sie von ihm überspringen zu lassen. Aber das wird sich dem Zuschauer doch nur als ein Unterschied des Grades zeigen, denn sowohl in A als auch in B verliert ja Einer endlich alle Steine, und eine nachlässig gespielte Partie des Spiels A braucht sich von einer solchen des Spiels B kaum, oder nicht, zu unterscheiden. – „Aber die Partie A wird sich doch nun von der Partie B im Geist in dem sie gespielt werden unterscheiden!” – Gewiß: die Spieler werden im allgemeinen bei ähnlichen äußeren Anlässen in den beiden Partien andere Gefühle haben; und der Zuschauer wird ja auch sehen, daß in B der Eine dem Andern einen Stein mit triumphierender Miene zuschiebt und der Andre ihn wenig erfreut überspringt; oder daß in A Einer unangenehm überrascht ist, wenn ihm der Andre einen Stein nimmt; daß er zögert, wenn er einen Stein dem Überspringen aussetzen muß; u.s.f.. Endlich wird der Zuschauer sehn, daß in A der, der seinen letzten Stein verloren hat dem Andern Geld gibt, oder sagt, er habe verloren, oder mit einer Miene der Ergebung in sein Schicksal vom Spiel aufsteht, der Andre aber mit einem schlecht unterdrückten Ausdruck der Befriedigung; u.s.f.. Aber sind denn die Gefühle immer die gleichen? Triumphiert jeder, der in A dem Andern einen Stein nimmt, oder sträubt sich jeder der ein Spiel verliert? Freut sich nicht Mancher über den Sieg des Andern? – Wie ist es also mit dem Unterschied des Geistes der beiden Partien? Ist es nicht so: Der Unterschied, kann man sagen, ist etwa so groß, wie der Unterschied im Ausdruck der Gemütsbewegung, die der Zuschauer beobachten kann; und im allgemeinen beobachten wird. Von dem Verhältnis der ‚Gemütsbewegung’ zu ‚ihrem Ausdruck’ wollen wir jetzt nicht reden. Wenn wir also die Partie als eine Handlung betrachten, so können wir sagen, daß sich im allgemeinen eine Partie A von einer Partie B unterscheiden wird durch die Art der Züge sowohl, als auch durch das was sonst während der Partie vorgeht; daß aber in einem besondern Fall der Unterschied bis auf ‚unwesentliche Äußerlichkeiten’ herabsinken kann, etwa darauf, daß ein Spieler vor Anfang der Partie sagt „Wir wollen eine Partie A spielen”. Der Zuschauer wird ferner einen Unterschied in den Regelverzeichnissen der beiden Spiele sehn.
1 [niedrigere| geringere]
2 [der| dieser]
-
145

-
Wir wollen nun Sprachspiele, von denen wir sagen würden, sie verwenden eine begrenzte Reihe von Zahlzeichen, mit solchen vergleichen, von denen wir sagen würden, sie verwenden eine unbegrenzte Reihe von Zahlzeichen.
-

-
Wie (3). A befiehlt B, ihm eine Anzahl von Bausteinen von bestimmter Form zu bringen. Die Zahlzeichen gibt A mit den Fingern der beiden Hände. Die Zahlzeichen sind zehn Bilder der beiden Hände mit gestreckten und eingebogenen Fingern. A gibt B den Befehl, indem er ihm ein solches Bild zeigt und dabei das Wort ‚Würfel’ oder ‚Platte’, etc. ausruft.
-

-
Wie (2). Die Reihe der Zahlwörter wird auswendig gelernt. In dem Befehl werden die Zahlwörter gerufen. Das Kind lernt sie durch mündlichen Unterricht.
-

-
Es wird eine Rechenmaschine (Abakus) verwendet. A stellt den Abakus und gibt ihn dem B. B geht damit dorthin wo die Platten liegen, etc.
-
146

-
B hat die Platten, die in Stößen liegen, zu zählen. Es geschieht mit einer Rechenmaschine; sie hat zwanzig Kugeln. In einem Stoß sind nie mehr als zwanzig Platten. B schiebt die Kugeln, den Platten eines Stoßes entsprechend, und zeigt darauf1 dem A die Rechenmaschine.
1 [dann| darauf]
-

-
Wie 30; der Abakus hat nun zwanzig kleine und eine große Kugel. Enthält der Stoß mehr als zwanzig Platten, so verschiebt B die große Kugel. (Sie entspricht also in gewisser Beziehung dem Wort ‚viele’.)
-

-
Wie 30. Wenn der Stoß n Platten enthält, wo n größer als 20 und kleiner als 40 ist, verschiebt B n-20 Kugeln, zeigt dem A die Rechenmaschine und klatscht dabei einmal in die Hände.
-

-
A und B verwenden die Zahlzeichen des Dezimalsystems (als Schrift- oder Lautzeichen) bis zu ‚20’. Das Kind lernt die Reihe dieser Zeichen auswendig; weiter wie in (2).
-

-
Ein gewisser Volksstamm besitzt eine Sprache von der Art (2). Die Zahlzeichen sind die Schriftzeichen unseres Dezimalsystems. Keines von ihnen ist als das höchste gekennzeichnet, wie z.B. in einigen der früher beschriebenen Spiele. (Man ist hier vielleicht versucht, fortzufahren: „obwohl natürlich eines von ihnen das höchste der tatsächlich gebrauchten Zahlzeichen ist”.)1 Die Kinder dieses Stammes lernen die Zahlzeichen auf folgende Weise: Man lehrt sie die Ziffern von ‚1’ bis ‚20’, wie in (2) die Wörter von ‚eins’ bis ‚zehn’. Und mit ihnen zählen sie Reihen von Gegenständen bis zu zwanzig auf den Befehl „Zähle diese Platten!”, „Zähle diese Würfel!”, etc. Später legt man ihnen eine Reihe von 21 Dingen vor und gibt wieder den Befehl ‚Zähle!’. Wenn nun das Kind beim Zählen bis zu ‚20’ gekommen ist macht der Lehrer eine Handbewegung, die das ‚Fortfahren’ andeutet, worauf das Kind, für gewöhnlich, die Ziffer ‚21’ schreibt. Ähnlich läßt man die Kinder bis ‚22’, und weiter, zählen. Bei diesen Übungen spielt keine Zahl die ausgesprochene Rolle der höchsten. Endlich muß das Kind Reihen von weit über 20 Gegenständen zählen, ohne die Nachhilfe des Lehrers. Macht ein Kind den Übergang ‚20’-‚21’ auf die suggestive Geste des Lehrers hin nicht, so wird es als schwachsinnig behandelt2.
1 [höchst gebrauchte ist”.)| höchste der tatsächlich gebrauchten Zahlzeichen ist”.)]
2 [gilt es als schwachsinnig| wird es als schwachsinnig behandelt]
-
147

-
Ein andrer Volksstamm: seine Sprache ist wie die in (34). Man beobachtet nicht, daß die Leute höher als bis 159 zählen. – Im Leben dieses Stammes spielt das Zeichen ‚159’ eine eigentümliche Rolle. – – Nehmen wir an, ich sagte: „Sie behandeln dieses Zahlzeichen als ihr höchstes”. – Aber was heißt das? – „Nun, sie sagen einfach es sei das höchste.”–
Aber wie: Sie sagen gewisse Worte – aber wie wissen wir, was sie damit meinen? Ein Kriterium dafür, was sie meinen, wären die Gelegenheiten bei denen sie das Wort aussprechen, welches wir mit unserm „höchste” übersetzen wollen, die Rolle welche jenes Wort im Leben des Stammes spielt. Wir können uns leicht das Zahlzeichen ‚159’ bei solchen Anlässen, in Verbindung mit solchen Gesten und Formen des Benehmens gebraucht denken, daß wir sagen müßten, dieses Zeichen spiele bei ihnen die Rolle einer unübersteigbaren oberen Grenze. Selbst dann, wenn der Stamm kein Wort besäße, welches unserm „höchste” entspricht, und das Kriterium dafür, daß ‚159’ das höchste Zahlzeichen ist, in nichts läge, was sie darüber sagen.
-
148

-
Ein Stamm besitzt zwei Systeme des Zählens: Man lernt Zählen mit den Buchstaben des Alphabets, und außerdem mit den Zahlzeichen des Dezimalsystems, wie in (34). Die erste Art nennen sie die ‚offene’ Art des Zählens, die zweite die ‚geschlossene’ und sie verwenden diese beiden Wörter auch für eine offene und geschlossene Türe.
-

-
In (27) ist die Reihe der Zahlzeichen in augenfälliger Weise beschränkt. – In (27) und (28) ist ein ‚beschränkter Vorrat’ von Zahlzeichen vorhanden: denke an die Analogie dieser beiden Beschränkungen, und wieder an den Mangel der Analogie. – In (30) liegt die Beschränkung einerseits im Werkzeug des Zählens. Dann aber, in ganz anderer Weise, darin, daß nie mehr als zwanzig Gegenstände gezählt werden. – In (31) fehlt diese Beschränkung, aber die große Kugel an der Rechenmaschine betont die Beschränkung unserer Mittel. – Ist (32) ein beschränktes oder unbeschränktes Spiel? Die Praxis der Anwendung des Abakus, die wir beschrieben haben, hat 40 als Grenze. – Wir sind geneigt zu sagen, dieses Spiel ‚hat es in sich’, unbegrenzt fortgesetzt werden zu können.1 Aber vergessen wir nicht, daß wir auch die vorhergehenden Spiele als Anfänge endloser Systeme hätten auffassen können. – In (33) tritt das Systematische, d.h. die Gesetzmäßigkeit, in den Zahlzeichen noch augenfälliger hervor2. Hier wäre man geneigt zu sagen, es sei dem Spiel durch das Werkzeug des Zählens keine Grenze gesetzt; wenn nicht die Kinder die Zahlwörter von ‚1’ bis ‚20’ auswendig lernten. Das legt den Ausdruck nahe3, daß sie nicht lernen, das System zu ‚verstehen’, welches wir in diesen Zahlzeichen sehen. – Von den Leuten in (34) werden wir sagen, sie verwenden ein unbegrenztes System von Zahlzeichen, sie kennen die unendliche Kardinalzahlenreihe. – (35) kann uns zeigen, welche ungeheure Mannigfaltigkeit von Fällen man sich denken kann, in denen man geneigt wäre4 zu sagen, die Arithmetik der Leute bediene sich einer endlichen Zahlenreihe, obwohl der Unterricht im Gebrauch der Zahlzeichen keines als obere Grenze hinstellt. – In (36) bedient sich die Sprache des Stammes selbst der Wörter ‚offen’ und ‚geschlossen’ (statt deren wir durch eine geringfügige Veränderung des Beispiels die Wörter ‚begrenzt’ und ‚unbegrenzt’ setzen konnten). In dieser einfachen und klar umschriebenen Form gebraucht ist natürlich gar nichts Geheimnisvolles an der Verwendung5 des Wortes ‚offen’. Aber dieses Wort entspricht unserm ‚unendlich’, und die Verwendung dieses Wortes ist nur ungeheuer viel komplizierter, als die des Wortes6 ‚offen’. Das heißt, die Bedeutung von ‚unendlich’ ist ebenso wenig geheimnisvoll7, als die von ‚offen’, und die Idee, sie sei in irgend einem Sinne transzendent beruht auf einem Mißverständnis.
1 [daß es unbegrenzt fortgesetzt werden kann.| unbegrenzt fortgesetzt werden zu können.]
2 [ist das System, d.h. die Gesetzmäßigkeit, in den Zahlzeichen noch augenfälliger| tritt das Systematische, d.h. die Gesetzmäßigkeit, in den Zahlzeichen noch augenfälliger hervor]
3 [die Auffassung nahe| den Ausdruck nahe]
4 [wir geneigt wären| man geneigt wäre]
5 [Bedeutung| Verwendung]
6 [von| des Wortes]
7 [ungeheimnisvoll| wenig geheimnisvoll]
-

Next part
Return to menue of available texts
The Wittgenstein Archives at the University of Bergen
Harald Haarfagresgate 31, N-5007 Bergen, NORWAY
Page last updated: 15. April 1996
 Franz Hespe
Franz Hespe



















































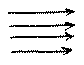
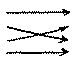
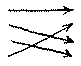 etc.
etc.
















 Franz Hespe
Franz Hespe